月の中心差の黄経不等は、サインカーブで良いのか(長さん)
国立天文台暦計算室のページその他で、月の黄経
不等の第1項の中心差は、約6°.3の振幅の、
サインカーブだと書いてある。今回は疑うわけで
はないが、本当にサインカーブになるのかどうか
をチェックしてみた。ただし、今までの議論と同
じく軌道傾斜角は0°に近く、離心率も0に近く、
1からは遠い月の軌道について考える。なおこの
考察は藤原京時代の囲碁の隆盛の原因を、定朔法
の暦、儀鳳暦の日本に於ける7世紀の採用に、関
連付けるためにしている。
結論は証明するのが
私にはしんどかったが、合っていた。
では、議論を開始する。
ポイントは、軌道傾斜が0°で、不等がまるご
と、近点角偏差から来る場合だけ考える、単純化
をしても平均近点角から真近点角に変換するのに、
途中に離心近点角を経由しなければならない事
だ。結論から述べると、
真近点角偏差=(1+asin(θ))×(1+bsin(θ))
≒1+(a+b)×sin(θ)
だから、サインカーブになるという論理だが、
(1+asin(θ)の証明は簡単だが、
(1+bsin(θ))の証明が結構難しい
というパターンという意味である。蛇足だが、
プトレマイオスがエカントという、奇妙な概念を
考えたのは、aとbが比較的近く、軌道離心率e
にも近いためである。
戻すと(1+asin(θ))側の証明は、
ケプラーの方程式が、
M=E-esinE
でEが求める離心近点角だが、離心率が小さい月
の軌道では、平均近点角Mとの間に、M≒Eが成
り立つので、
E≒M+esinM
であるで証明はおしまいである。(eは離心率で
月では、5%の桁だ。)
ところが(1+bsin(θ))側の方は、
tan(真近点角/2)=√(1+e)/(1-e)×tan(E/2)
という形になっている。真近点角(ラジアン)=・・・
という式は、成書には載っていない。なお、真近
点角(ラジアン)時間微分=・・・という式が、
木下宙氏の成書”天体と軌道の力学”に有ったが、
私には理解できなかった。
自分で解けば良いではないかと言われれば、そ
れまでだが。考えているうちに、私は正直嫌気が
差したので、数値計算に切り替えた。国立大学へ
の大学受験生程度の数学力が有れば、この問題は
すらすら解けたであろう。
ともあれ結果は、以下の図のようになった。
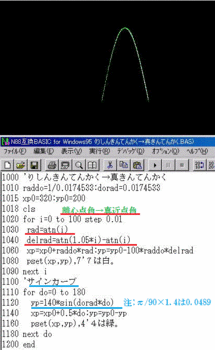
なおこの問題に限っては、定義となる図形に戻っ
て、日がな一日のんびりと、その図を眺めていれ
ば、そうしていたら、私でも解けていたのかもし
れないと、後付けで気がついた。
ともあれ確かに、離心近点角から真近点角への
変換も、差分はsinカーブになっているようだ。
そこで、
平均近点角から真近点角への変換で、偏差は離心
率が小さい軌道では総合的に、sinカーブにな
ると見てよさそうだ。
以上のように、冒頭で述べた通り、私にもやっと
こさっとこ、理解できたという次第である。
(2020/05/20)
不等の第1項の中心差は、約6°.3の振幅の、
サインカーブだと書いてある。今回は疑うわけで
はないが、本当にサインカーブになるのかどうか
をチェックしてみた。ただし、今までの議論と同
じく軌道傾斜角は0°に近く、離心率も0に近く、
1からは遠い月の軌道について考える。なおこの
考察は藤原京時代の囲碁の隆盛の原因を、定朔法
の暦、儀鳳暦の日本に於ける7世紀の採用に、関
連付けるためにしている。
結論は証明するのが
私にはしんどかったが、合っていた。
では、議論を開始する。
ポイントは、軌道傾斜が0°で、不等がまるご
と、近点角偏差から来る場合だけ考える、単純化
をしても平均近点角から真近点角に変換するのに、
途中に離心近点角を経由しなければならない事
だ。結論から述べると、
真近点角偏差=(1+asin(θ))×(1+bsin(θ))
≒1+(a+b)×sin(θ)
だから、サインカーブになるという論理だが、
(1+asin(θ)の証明は簡単だが、
(1+bsin(θ))の証明が結構難しい
というパターンという意味である。蛇足だが、
プトレマイオスがエカントという、奇妙な概念を
考えたのは、aとbが比較的近く、軌道離心率e
にも近いためである。
戻すと(1+asin(θ))側の証明は、
ケプラーの方程式が、
M=E-esinE
でEが求める離心近点角だが、離心率が小さい月
の軌道では、平均近点角Mとの間に、M≒Eが成
り立つので、
E≒M+esinM
であるで証明はおしまいである。(eは離心率で
月では、5%の桁だ。)
ところが(1+bsin(θ))側の方は、
tan(真近点角/2)=√(1+e)/(1-e)×tan(E/2)
という形になっている。真近点角(ラジアン)=・・・
という式は、成書には載っていない。なお、真近
点角(ラジアン)時間微分=・・・という式が、
木下宙氏の成書”天体と軌道の力学”に有ったが、
私には理解できなかった。
自分で解けば良いではないかと言われれば、そ
れまでだが。考えているうちに、私は正直嫌気が
差したので、数値計算に切り替えた。国立大学へ
の大学受験生程度の数学力が有れば、この問題は
すらすら解けたであろう。
ともあれ結果は、以下の図のようになった。

なおこの問題に限っては、定義となる図形に戻っ
て、日がな一日のんびりと、その図を眺めていれ
ば、そうしていたら、私でも解けていたのかもし
れないと、後付けで気がついた。
ともあれ確かに、離心近点角から真近点角への
変換も、差分はsinカーブになっているようだ。
そこで、
平均近点角から真近点角への変換で、偏差は離心
率が小さい軌道では総合的に、sinカーブにな
ると見てよさそうだ。
以上のように、冒頭で述べた通り、私にもやっと
こさっとこ、理解できたという次第である。
(2020/05/20)







