宮城県多賀城市新田遺跡より将棋駒状物品(長さん)
奈良文化財研究所の発掘報告書のデータベース
全国遺跡報告総覧のデータベースの中の幾つかに、
今回問題にする、宮城県多賀城市新田遺跡の
14世紀初の”出土駒”が言及されている。
が、形こそ将棋駒だが、
疑わしいという報告をする。
つまり、
上部に穴の跡があり何らかのフダの可能性が有る
ようだ。では論を続ける。
奈良文化財研究所の発掘報告書のデータベース
は次の通りである。
全国遺跡報告総覧のデータベース(urlは、
https://sitereports.nabunken.go.jp/ja)
この中に、次のpdfファイル名で、問題の
遺物の紹介された、発掘報告書が載っている。
9690_1_新田遺跡.pdf
発掘報告書の名称は、次の通りである。
(宮城県)多賀城市文化財調査報告書第23集
新田遺跡、(第4次・第11次報告書)、
西暦1990年、多賀城市埋蔵文化財調査センター。
そこの108ページに、”将棋駒”のスケッチ
があるが、
上部に穴の跡が記載され、駒名は無い。
確かに形は中世南北朝時代風の将棋駒型である。
従って、あくまで本ブログの見解だが、
何らかの荷札類であって、将棋駒では無い疑い
を持ったほうが良い
と思う。205ページ付近に、図版37が
あり出土駒の写真も発掘報告書には載っている。
しかし、そこにも上部に穴跡が判り、駒名は
ざっと見だが、私には良く判らない。

たぶんだが、何らかの札用として、将棋駒用
の木片を使ったのだろうが。将棋駒では無い
可能性が、このケースは結構有るのでは無いか
と、私は疑っている。中世も前期に遡る可能性
が有りそうだが、将棋駒では無かったとすれば
無念である。(2020/06/30)
全国遺跡報告総覧のデータベースの中の幾つかに、
今回問題にする、宮城県多賀城市新田遺跡の
14世紀初の”出土駒”が言及されている。
が、形こそ将棋駒だが、
疑わしいという報告をする。
つまり、
上部に穴の跡があり何らかのフダの可能性が有る
ようだ。では論を続ける。
奈良文化財研究所の発掘報告書のデータベース
は次の通りである。
全国遺跡報告総覧のデータベース(urlは、
https://sitereports.nabunken.go.jp/ja)
この中に、次のpdfファイル名で、問題の
遺物の紹介された、発掘報告書が載っている。
9690_1_新田遺跡.pdf
発掘報告書の名称は、次の通りである。
(宮城県)多賀城市文化財調査報告書第23集
新田遺跡、(第4次・第11次報告書)、
西暦1990年、多賀城市埋蔵文化財調査センター。
そこの108ページに、”将棋駒”のスケッチ
があるが、
上部に穴の跡が記載され、駒名は無い。
確かに形は中世南北朝時代風の将棋駒型である。
従って、あくまで本ブログの見解だが、
何らかの荷札類であって、将棋駒では無い疑い
を持ったほうが良い
と思う。205ページ付近に、図版37が
あり出土駒の写真も発掘報告書には載っている。
しかし、そこにも上部に穴跡が判り、駒名は
ざっと見だが、私には良く判らない。

たぶんだが、何らかの札用として、将棋駒用
の木片を使ったのだろうが。将棋駒では無い
可能性が、このケースは結構有るのでは無いか
と、私は疑っている。中世も前期に遡る可能性
が有りそうだが、将棋駒では無かったとすれば
無念である。(2020/06/30)
山梨県鰍沢町鰍沢河岸跡より、磁器製の桂馬駒(長さん)
以前に山梨県の出土史料として、甲府市の甲府
城下町遺跡の、中将棋駒(?)3枚出土を紹介
した事が有った。その後、奈良文化財研究所の
発掘報告書のデータベース
全国遺跡報告総覧のデータベース(urlは、
https://sitereports.nabunken.go.jp/ja)
に、西暦2005年頃、別の出土史料が有るの
を発見した。pdfファイル名は、以下の通り
である。
6547_1_鰍沢河岸跡Ⅱ.pdf
発掘報告書の名称は以下の通り。
鰍沢河岸跡Ⅱ(第2分冊)、2005年3月、
山梨県教育委員会、国土交通省関東地方整備局。
”白子明神地区宅地水防災事業に伴う発掘調査
報告書”との事である。なお鰍沢河岸とは、
昭和の初期まであった山梨県南巨摩郡富士川町
の水運の拠点との事である。
上記の発掘報告書の573ページに磁器製の
桂馬駒の写真が載っている。

他の物品の様子から、江戸時代から近代初期・
昭和初期までのものであろうと、推測できる。
なお、同報告書にスケッチで、サイコロのよう
な遺物も載っている。賭博が行われたのであろ
う。
同報告書の10ページには駒のスケッチも載っ
ていて、問屋街地区(遺物)と記載されている。
江戸時代に、山梨県のこの界隈は、だいぶん
賑わっていたようだ。ともあれ、成りは普通の
桂馬の成りである、桂馬の裏崩しの”金”であ
るらしい。
ここへ来て、木製以外の将棋駒の出土例が、
少し増えてきた。何れにしても。
なんらかの遊具として、甲府盆地内の山梨県
南巨摩郡富士川町のこの遺跡では、かつて近世~
近代初期に瀬戸製将棋駒が使われていたらしい。
(2020/06/29)
城下町遺跡の、中将棋駒(?)3枚出土を紹介
した事が有った。その後、奈良文化財研究所の
発掘報告書のデータベース
全国遺跡報告総覧のデータベース(urlは、
https://sitereports.nabunken.go.jp/ja)
に、西暦2005年頃、別の出土史料が有るの
を発見した。pdfファイル名は、以下の通り
である。
6547_1_鰍沢河岸跡Ⅱ.pdf
発掘報告書の名称は以下の通り。
鰍沢河岸跡Ⅱ(第2分冊)、2005年3月、
山梨県教育委員会、国土交通省関東地方整備局。
”白子明神地区宅地水防災事業に伴う発掘調査
報告書”との事である。なお鰍沢河岸とは、
昭和の初期まであった山梨県南巨摩郡富士川町
の水運の拠点との事である。
上記の発掘報告書の573ページに磁器製の
桂馬駒の写真が載っている。

他の物品の様子から、江戸時代から近代初期・
昭和初期までのものであろうと、推測できる。
なお、同報告書にスケッチで、サイコロのよう
な遺物も載っている。賭博が行われたのであろ
う。
同報告書の10ページには駒のスケッチも載っ
ていて、問屋街地区(遺物)と記載されている。
江戸時代に、山梨県のこの界隈は、だいぶん
賑わっていたようだ。ともあれ、成りは普通の
桂馬の成りである、桂馬の裏崩しの”金”であ
るらしい。
ここへ来て、木製以外の将棋駒の出土例が、
少し増えてきた。何れにしても。
なんらかの遊具として、甲府盆地内の山梨県
南巨摩郡富士川町のこの遺跡では、かつて近世~
近代初期に瀬戸製将棋駒が使われていたらしい。
(2020/06/29)
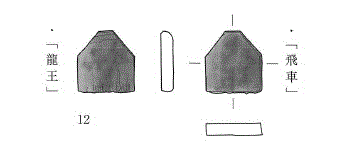
仙台城より、成り龍王飛車駒が追加出土(長さん)
本件も以前のと同様、発掘調査報告書が
奈良文化財研究所の、全国遺跡報告総覧のデータ
ベース(urlは、https://sitereports.nabunken.go.jp/ja)
の中にありweb上に公開されている。
ただし、pdfファイル名から個別の
発掘調査報告書ではなくて、
東北大学埋蔵文化財調査室の2007年の年報
の中の、記事である事が判る。遺跡の場所は、
仙台城周辺の、武家屋敷内のようである。
pdfファイル名は、次の通り。
10034_1_東北大学埋蔵文化財調査年報.pdf
仙台城からは天童の将棋駒と全国遺跡出土駒
(2003、山形県天童市の天童市将棋資料館)
に有るように、成りと(金)一文字”兵”駒お
よび、不成り玉将駒(何れも、駒の動かし方打
点付き)が、出土している事で著名である。
今回は場所が少し違うし、遺物も、
木製の6角形駒
である。飛車には間違い無さそうだが、使用し
た人間は、仙台城本丸跡の玉将や兵とは、ぜん
ぜん別人なのであろう。
他に、享保の年号の入った木簡が複数出土して
いるとの事なので、形からは判別困難だが、将
棋駒は、江戸時代の成立に、間違いは無さそう
である。
更に、同報告書の125ページには、将棋駒
の形ではないが、
木簡に”金将”と書かれたものが発見
されているとの旨写真が紹介されているようだ。
用途は不明だが、棋譜を木札に書いて、将棋の
研究に使ったのかもしれない。
何れにしても、仙台藩の城下町には江戸時代、
将棋の高段者や、研究会等が在野で存在したの
であろう。(2020/06/28)
奈良文化財研究所の、全国遺跡報告総覧のデータ
ベース(urlは、https://sitereports.nabunken.go.jp/ja)
の中にありweb上に公開されている。
ただし、pdfファイル名から個別の
発掘調査報告書ではなくて、
東北大学埋蔵文化財調査室の2007年の年報
の中の、記事である事が判る。遺跡の場所は、
仙台城周辺の、武家屋敷内のようである。
pdfファイル名は、次の通り。
10034_1_東北大学埋蔵文化財調査年報.pdf
仙台城からは天童の将棋駒と全国遺跡出土駒
(2003、山形県天童市の天童市将棋資料館)
に有るように、成りと(金)一文字”兵”駒お
よび、不成り玉将駒(何れも、駒の動かし方打
点付き)が、出土している事で著名である。
今回は場所が少し違うし、遺物も、
木製の6角形駒
である。飛車には間違い無さそうだが、使用し
た人間は、仙台城本丸跡の玉将や兵とは、ぜん
ぜん別人なのであろう。

他に、享保の年号の入った木簡が複数出土して
いるとの事なので、形からは判別困難だが、将
棋駒は、江戸時代の成立に、間違いは無さそう
である。
更に、同報告書の125ページには、将棋駒
の形ではないが、
木簡に”金将”と書かれたものが発見
されているとの旨写真が紹介されているようだ。

用途は不明だが、棋譜を木札に書いて、将棋の
研究に使ったのかもしれない。
何れにしても、仙台藩の城下町には江戸時代、
将棋の高段者や、研究会等が在野で存在したの
であろう。(2020/06/28)
茨城県笠間市宍戸城遺跡より2006年頃金将駒(長さん)
以前述べた出土駒と同様、表題の発掘調査報告書
が奈良文化財研究所の全国遺跡報告総覧のデータ
ベース(urlは、https://sitereports.nabunken.go.jp/ja)
の中にあり、web上に公開されている。
今回は、茨城県での出土である。
web上にあるpdfのファイル名は以下の通り。
11960_1_新善光寺跡宍戸城跡.pdf
発掘報告書の題名は、次の通りである。
茨城県教育財団文化財調査報告第256集
新善光寺跡、宍戸城跡
茨城県水戸土木事務所・財団法人茨城県教育財団
(西暦2006)。
形から、
近世の不成り金将駒のよう
である。

名称は宍戸城だが、江戸時代初期に、秋田氏が居
城していたとの説明が、発掘報告書の冒頭、6ペー
ジ付近にあるようだ。その時代のものかもしれな
い。
何れにしても、茨城県県内では、新旧を問わず、
珍しい将棋駒の出土例となった。(2020/06/26)
が奈良文化財研究所の全国遺跡報告総覧のデータ
ベース(urlは、https://sitereports.nabunken.go.jp/ja)
の中にあり、web上に公開されている。
今回は、茨城県での出土である。
web上にあるpdfのファイル名は以下の通り。
11960_1_新善光寺跡宍戸城跡.pdf
発掘報告書の題名は、次の通りである。
茨城県教育財団文化財調査報告第256集
新善光寺跡、宍戸城跡
茨城県水戸土木事務所・財団法人茨城県教育財団
(西暦2006)。
形から、
近世の不成り金将駒のよう
である。

名称は宍戸城だが、江戸時代初期に、秋田氏が居
城していたとの説明が、発掘報告書の冒頭、6ペー
ジ付近にあるようだ。その時代のものかもしれな
い。
何れにしても、茨城県県内では、新旧を問わず、
珍しい将棋駒の出土例となった。(2020/06/26)
(コラム)パソコンが故障(長さん)
以下、マイクロソフトは緊急事態に頼りにならない
という話をする。バックアップツールの
aomeiバックアッパーに助けられたという話題
である。
通常使用しているパソコンが、3日前程度に、
液晶のライン抜けを起こすようになった。パソコン
の不良品とは考えられない。中古である上に、数年
激しく使い込んだからである。なお最近、手荒に扱っ
た記憶はない。
かなり前だが、私は、
全く型番まで一緒のパソコンを予備に用意していた。
しかも、windows7は、リカバリーディスク
を持っている。ただし理由は私には良く判らないが、
プロダクトキーが買ったときから記載されていない。
とりあえず、osをインストールすると、
ソフトがニセモノだから、オンラインで認証せよ
と出る。しかし私はこれを、windows7の
予備パソコンへのインスト時から拒否した。ウィルス
にやられて、第1使用システムをダウンさせたあと
で、第2システムをオンライン時に、同じウィルス
に感染させたら、共倒れだからだ。
つまり、第2予備パソコンは、スタンドアローンの
まま、妙なメッセージを発するosを載せたままで
放置して来た
のである。理由は、どうでもよかったからだ。しか
し、今回、その第2予備システムを使わなければ、
不便になった。
幸い、
タスクバーを上に持ってくれば、ライン抜けの有る
第1メインパソコンは、使える状態だった。
ので、今回話題の、aomeiバックアッパーを
ダウンロードして、
本来は、パソコン、usbの間でデータをやり取り
するだけなのだろうが、コピーしておいて、予備
パソコンに、試しにまるごとリストア復元してみた。
windowsの使い方としてアウトローだが、
ハードが周辺機器をつけていないという点を含めて
いっしょだったので、何とか見かけ同じになった。
そこでこの記事は、その予備の新しい同じ型番の、
パソコンで、書いてブログに書き込んでいる。
マイクロソフト側としては言い分があるのだろう
が。そもそも、
緊急事態のときに、スペアが使用できるようにする
という考え方が、妨害されるのは事実なので、
この会社のやり方は、私にはちょっと頂けない。
それに対し、バックアッパーだったのだろうが、
コピーも出来たaomeiソフトには、現実として
今回たいへん助けられた。
そもそも、
windows7の上で、アプリケーションが走っ
て居なくても、ユーザーにとっては、パソコンが突
然壊れたときに、
環境が変わらないので、いつものようにwebに
繋げるスペアが使えれば、それで良いという着想が
マイクロソフト社には欠けていて、aomeiには
それも有った
ように、私には思えた。
それにそもそも、私のosのwindows7は、
たった13年で、マイクロソフトがサポート自体を
やめてしまった程度のものである。
また、
バックアッパーを使う作業に、現実1時間は要し、
aomeiバックアップツールを、不正用途に使用
する事を常態化させるという発想の可能性自体、
非現実感満載ではないかと作業してみて私は感じた。
以上の書き込みを、マイクロソフトの関係者がもし
見ていて、何か言いたいことがあれば、この記事の
コメントにでも、ぜひ書いてもらいたいものだ。
なお予備パソコンをnet接続した状態の感触だが、
追跡防止のeasyリストが、正常に働いていない
ように私には見える。
前の壊れかけパソコンと、接続交換する等して、
良く調べてみるつもりだ。何れにしても、このよう
に非常時にはたいへんな状況なので、”オンライン
世界が、現実世界にとって変わる”可能性など、絵
に描いた餅である事だけは確かだと、私は確信する。
(2020/06/26 その2)
という話をする。バックアップツールの
aomeiバックアッパーに助けられたという話題
である。
通常使用しているパソコンが、3日前程度に、
液晶のライン抜けを起こすようになった。パソコン
の不良品とは考えられない。中古である上に、数年
激しく使い込んだからである。なお最近、手荒に扱っ
た記憶はない。
かなり前だが、私は、
全く型番まで一緒のパソコンを予備に用意していた。
しかも、windows7は、リカバリーディスク
を持っている。ただし理由は私には良く判らないが、
プロダクトキーが買ったときから記載されていない。
とりあえず、osをインストールすると、
ソフトがニセモノだから、オンラインで認証せよ
と出る。しかし私はこれを、windows7の
予備パソコンへのインスト時から拒否した。ウィルス
にやられて、第1使用システムをダウンさせたあと
で、第2システムをオンライン時に、同じウィルス
に感染させたら、共倒れだからだ。
つまり、第2予備パソコンは、スタンドアローンの
まま、妙なメッセージを発するosを載せたままで
放置して来た
のである。理由は、どうでもよかったからだ。しか
し、今回、その第2予備システムを使わなければ、
不便になった。
幸い、
タスクバーを上に持ってくれば、ライン抜けの有る
第1メインパソコンは、使える状態だった。
ので、今回話題の、aomeiバックアッパーを
ダウンロードして、
本来は、パソコン、usbの間でデータをやり取り
するだけなのだろうが、コピーしておいて、予備
パソコンに、試しにまるごとリストア復元してみた。
windowsの使い方としてアウトローだが、
ハードが周辺機器をつけていないという点を含めて
いっしょだったので、何とか見かけ同じになった。
そこでこの記事は、その予備の新しい同じ型番の、
パソコンで、書いてブログに書き込んでいる。
マイクロソフト側としては言い分があるのだろう
が。そもそも、
緊急事態のときに、スペアが使用できるようにする
という考え方が、妨害されるのは事実なので、
この会社のやり方は、私にはちょっと頂けない。
それに対し、バックアッパーだったのだろうが、
コピーも出来たaomeiソフトには、現実として
今回たいへん助けられた。
そもそも、
windows7の上で、アプリケーションが走っ
て居なくても、ユーザーにとっては、パソコンが突
然壊れたときに、
環境が変わらないので、いつものようにwebに
繋げるスペアが使えれば、それで良いという着想が
マイクロソフト社には欠けていて、aomeiには
それも有った
ように、私には思えた。
それにそもそも、私のosのwindows7は、
たった13年で、マイクロソフトがサポート自体を
やめてしまった程度のものである。
また、
バックアッパーを使う作業に、現実1時間は要し、
aomeiバックアップツールを、不正用途に使用
する事を常態化させるという発想の可能性自体、
非現実感満載ではないかと作業してみて私は感じた。
以上の書き込みを、マイクロソフトの関係者がもし
見ていて、何か言いたいことがあれば、この記事の
コメントにでも、ぜひ書いてもらいたいものだ。
なお予備パソコンをnet接続した状態の感触だが、
追跡防止のeasyリストが、正常に働いていない
ように私には見える。
前の壊れかけパソコンと、接続交換する等して、
良く調べてみるつもりだ。何れにしても、このよう
に非常時にはたいへんな状況なので、”オンライン
世界が、現実世界にとって変わる”可能性など、絵
に描いた餅である事だけは確かだと、私は確信する。
(2020/06/26 その2)
距離の2乗(a^2-2ab+b^2)暗算の別法(長さん)
以前、座標計算の方法について論じたときに、
出発点から、最接近点までの距離をa、
出発点から、排除域限界円までの距離をx、
排除域限界円から最接近点までの距離をbとして
距離xを未知数とし、
x=a-bなのだが、実際には
a^2が求まっていて、aには計算誤差がある為、
X^2=a^2-2ab+b^2を、迂回して
暗算で求める
事を議論した。なお、0.7^2≒0.5は、この
ケースはたまたま、とても簡単になっている。そ
こでそのときに、近似的なa=√a^2は、
頭の中で求めることになるとしたが、
この計算が面倒だったとしたら、他に方法は無
いのか
について、その後再考した。
結論は、
有る
で、方法は、
常用対数の数値を、有る程度覚えていて、
a^2とb^2を常用対数化して、2(√a^2×b^2)
を求める
となった。
では、議論を開始する。
覚える必要のある数字は、以下のものだとみら
れる。
2の常用対数:0.3010
3の常用対数:0.4771
更に、次の数を加えておく。
7の常用対数:0.8451
逆に、次の知見が必要とみられる。
常用対数0.1の真数:1.26
常用対数0.2の真数:1.59(←今回使用)
常用対数0.4の真数:2.51
常用対数0.8の真数:6.30
なお、最後の2つは、星の等級の階差として
有名。だが2.5より0.01大きい事は、
余り知られていない。
以上程度である。例として、以前に行った計算
を繰り返してみる。
a^2=5.276
b^2=0.5-0.024=0.476
で排除域限界円までの、自駒出発点からの距離
の2乗、x^2を求めるケースであった。
≒5.276-2×{√5.276×(0.5-0.024)}+(0.5-0.024)
=5.276-2×(√5.276×0.476)+0.476
これを前は、
≒5.276-2×2.3×0.7+0.476
としたが、(√5.276×0.476)の部分
を対数で出してみる。まず、
5.276の常用対数:0.7+0.3×0.08(程度)
≒0.724
次に、
0.476の常用対数:-1+0.7-0.24×0.1(程度)
≒-1+0.676
なお、上の階差が0.08程度なのは6の常用対
数が、0.7781程度で5の場合と0.08程度
の差であるため。
下の階差が0.1なのは、4の常用対数が
0.6020で、5の場合と0.1程度の差であ
るためである。
そこで平均をとると、:0.724+0.676-1=
0.4で、その1/2は0.2である。よって、
真数は1.59前後となり、1.61とした上の
計算とほぼ合う。このやり方の場合、
平方根を求める部分が無い。
そこで以下は、
≒5.276-3.18+0.476
=2.096+0.476
=2.572
となって、以前述べた、
≒5.276-3.22+0.476
=2.056+0.476
=2.532
という計算とは、大差の無い結果となる。
今の説明は、少し細かくしたので、頭の中の
暗算だと、私程度のレベルでは、少しキツイ感じ
もする。が、
{√5.276×(0.5-0.024)}が、
対数経由計算の結果、平方根計算部分が、
0.4/2=0.2で、真数1.59程度と、
簡単に出てしまうと、かなり楽な感じがする。
電卓で計算すると-3.18ないし-3.22
の部分は本当は、-3.16946であり、
2.58253が正しく、対数計算の方が良い。
何れにしても、a^2とb^2の幾何平均が、
a×bなので、このケースはa×bは
常用対数に直せば、平方根計算は経由しなかった
という知見は、落すべきではなかった。そのため
私は今回、己の数学的力の無さを、かなり反省さ
せられる事になった。(2020/06/26)
出発点から、最接近点までの距離をa、
出発点から、排除域限界円までの距離をx、
排除域限界円から最接近点までの距離をbとして
距離xを未知数とし、
x=a-bなのだが、実際には
a^2が求まっていて、aには計算誤差がある為、
X^2=a^2-2ab+b^2を、迂回して
暗算で求める
事を議論した。なお、0.7^2≒0.5は、この
ケースはたまたま、とても簡単になっている。そ
こでそのときに、近似的なa=√a^2は、
頭の中で求めることになるとしたが、
この計算が面倒だったとしたら、他に方法は無
いのか
について、その後再考した。
結論は、
有る
で、方法は、
常用対数の数値を、有る程度覚えていて、
a^2とb^2を常用対数化して、2(√a^2×b^2)
を求める
となった。
では、議論を開始する。
覚える必要のある数字は、以下のものだとみら
れる。
2の常用対数:0.3010
3の常用対数:0.4771
更に、次の数を加えておく。
7の常用対数:0.8451
逆に、次の知見が必要とみられる。
常用対数0.1の真数:1.26
常用対数0.2の真数:1.59(←今回使用)
常用対数0.4の真数:2.51
常用対数0.8の真数:6.30
なお、最後の2つは、星の等級の階差として
有名。だが2.5より0.01大きい事は、
余り知られていない。
以上程度である。例として、以前に行った計算
を繰り返してみる。
a^2=5.276
b^2=0.5-0.024=0.476
で排除域限界円までの、自駒出発点からの距離
の2乗、x^2を求めるケースであった。
≒5.276-2×{√5.276×(0.5-0.024)}+(0.5-0.024)
=5.276-2×(√5.276×0.476)+0.476
これを前は、
≒5.276-2×2.3×0.7+0.476
としたが、(√5.276×0.476)の部分
を対数で出してみる。まず、
5.276の常用対数:0.7+0.3×0.08(程度)
≒0.724
次に、
0.476の常用対数:-1+0.7-0.24×0.1(程度)
≒-1+0.676
なお、上の階差が0.08程度なのは6の常用対
数が、0.7781程度で5の場合と0.08程度
の差であるため。
下の階差が0.1なのは、4の常用対数が
0.6020で、5の場合と0.1程度の差であ
るためである。
そこで平均をとると、:0.724+0.676-1=
0.4で、その1/2は0.2である。よって、
真数は1.59前後となり、1.61とした上の
計算とほぼ合う。このやり方の場合、
平方根を求める部分が無い。
そこで以下は、
≒5.276-3.18+0.476
=2.096+0.476
=2.572
となって、以前述べた、
≒5.276-3.22+0.476
=2.056+0.476
=2.532
という計算とは、大差の無い結果となる。
今の説明は、少し細かくしたので、頭の中の
暗算だと、私程度のレベルでは、少しキツイ感じ
もする。が、
{√5.276×(0.5-0.024)}が、
対数経由計算の結果、平方根計算部分が、
0.4/2=0.2で、真数1.59程度と、
簡単に出てしまうと、かなり楽な感じがする。
電卓で計算すると-3.18ないし-3.22
の部分は本当は、-3.16946であり、
2.58253が正しく、対数計算の方が良い。
何れにしても、a^2とb^2の幾何平均が、
a×bなので、このケースはa×bは
常用対数に直せば、平方根計算は経由しなかった
という知見は、落すべきではなかった。そのため
私は今回、己の数学的力の無さを、かなり反省さ
せられる事になった。(2020/06/26)
愛媛県松山市小坂遺跡より石製将棋駒出土(長さん)
以下の発掘調査報告書が奈良文化財研究所の、
全国遺跡報告総覧のデータベース(urlは、
https://sitereports.nabunken.go.jp/ja)
の中にあり、web上に公開されているが、
表題愛知県松山市小坂遺跡より将棋駒が、西暦
2006年前後に出土している。公開されてい
るpdfのファイル名は、以下の通りである。
11576_2_束本遺跡9次・10次調査小坂遺跡1次~6次調査中村松田遺跡5.pdf
そこの118ページに将棋駒のスケッチ図が
記載されている。残念ながら、墨跡が消えてし
まい駒名は、判らないようである。報告書に、
複数の遺跡名が並んでいるが、小坂遺跡で西暦
2006年頃に発見されたようであり、
滑石(石製)であるとの旨が、114ページ
に書かれている。
成立期は、中世~近代という以外不明である。
発掘者は、江戸時代のものと見ているようであ
る。
前後したが、発掘報告書の書名は次の通り。
松山市文化財調査報告書153、
束本遺跡(-9次・10次調査)・小坂遺跡
(-1次~6次調査)・中村松田遺跡(-5次
・6次調査)、本文偏、2011年、
財団法人松山市文化・スポーツ振興財団、
埋蔵文化財センター
頭のトンガリが将棋駒にしてはやや鋭角で、
将棋駒を意識して作られた事は確かだが、
本当に将棋に使用したのかどうかは不明
ではないかと私見する。時代は極端に古い
可能性は少なそうである。当時から農村部で
あったとされており、何の為に作ったもの
か、にわかには判断しにくいと私は思うが。
不思議な物品が、愛媛で出土したものである。
(2020/06/25)
全国遺跡報告総覧のデータベース(urlは、
https://sitereports.nabunken.go.jp/ja)
の中にあり、web上に公開されているが、
表題愛知県松山市小坂遺跡より将棋駒が、西暦
2006年前後に出土している。公開されてい
るpdfのファイル名は、以下の通りである。
11576_2_束本遺跡9次・10次調査小坂遺跡1次~6次調査中村松田遺跡5.pdf
そこの118ページに将棋駒のスケッチ図が
記載されている。残念ながら、墨跡が消えてし
まい駒名は、判らないようである。報告書に、
複数の遺跡名が並んでいるが、小坂遺跡で西暦
2006年頃に発見されたようであり、
滑石(石製)であるとの旨が、114ページ
に書かれている。
成立期は、中世~近代という以外不明である。
発掘者は、江戸時代のものと見ているようであ
る。
前後したが、発掘報告書の書名は次の通り。
松山市文化財調査報告書153、
束本遺跡(-9次・10次調査)・小坂遺跡
(-1次~6次調査)・中村松田遺跡(-5次
・6次調査)、本文偏、2011年、
財団法人松山市文化・スポーツ振興財団、
埋蔵文化財センター
頭のトンガリが将棋駒にしてはやや鋭角で、
将棋駒を意識して作られた事は確かだが、
本当に将棋に使用したのかどうかは不明
ではないかと私見する。時代は極端に古い
可能性は少なそうである。当時から農村部で
あったとされており、何の為に作ったもの
か、にわかには判断しにくいと私は思うが。
不思議な物品が、愛媛で出土したものである。
(2020/06/25)
関数電卓、web情報、数表を使わずsinθを求める(長さん)
以前述べた通り、さいきん本ブログでは、座標の取り方
によらないゲームを考え、座標回転を議論している。通
常座標回転のsin(θ)cos(θ)は、関数電卓で
計算するのだが、ここでは簡便な筆算方法について考察
する。要旨から書く。sin(θ)を求めるとして、
60°から上と下とで分け、上は1-1/2θ^2方式
で、下は1+θ近似方式で求める。ただし、60°より
上については、最後に二次曲線から、はずれる部分を、
数値で微補正。
下については、傾きに係数を掛けて、折れ線近似で補
正してゆく。
では、以下に詳しく述べる。
まず、1°が0.0174533ラジアンである事、
つまりrad(1°)=0.0174533であり、
また次の数値は、覚える事にする。
sin(0°)=0.
sin(15°)=√6-√2/4=0.2588
sin(30°)=0.5000
sin(45°)=√2/2=0.7071
sin(60°)=√3/2=0.8660
sin(75°)=√6+√2/4=0.9659
sin(90°)=1
更に以下の数値を覚える事が、実際の計算では大切だ。
rad(1°)×sin(0°)×10^4=0
rad(1°)×sin(15°)×10^4=45.2
rad(1°)×sin(30°)×10^4=87.3
rad(1°)×sin(45°)×10^4=123.4
rad(1°)×sin(60°)×10^4=151.1
rad(1°)×sin(75°)×10^4=168.6
rad(1°)×sin(90°)×10^4=174.5
また、大事な定数は以下だ。
rad(1°)×rad(1°)×1/2×10^4=1.52
これらはこのケースは、座標回転の計算が実際に必
要なら、そのときには覚えるという覚悟を持てば、
使えるだろう。
まずは、座標を回転させる計算をするためには、
sin(θ)と、sin(90°-θ)を求める必
要がある。どちらの場合も、60°を境に上か下か
で、場合分けをする。
上の場合を先ず述べる。
sin(θ°)(90°>θ°>60°)として
sin(θ°)=sin(90°)-{rad(1°)×rad(1°)×1/2×10^4}×(θ°^2)×sin(90°)/10^4
=1-{rad(1°)×rad(1°)×1/2×10^4}×(θ°^2)/10^4
=1-1.52×(θ°^2)/10^4
これは、60°以上で、sin(θ)を90°を基
準に2次までテーラー展開しただけだ。当然90°
から離れると、かなりの誤差がある。それを、次の
ように補正する。
誤差がどの位かを、経験的に式で表す。つまり
誤差=-小数以下切捨て[10^{1/12*(78°-θ°)}]×10^(-4)
になると、考える。
だから、小数以下切捨て[10^{1/12*(78°-θ°)}]×10^(-4)
を足して補正する。ただし、90°から3°刻みで、
中心値で、代表させて良い。とどのつまり
小数以下切捨て[10^{1/12*(78°-θ°)}]×10^(-4)は、
θが77°以上では0×10^(-4)。
74°~77°(未満)では1×10^(-4)。
71°~74°(未満)では3×10^(-4)。
68°~71°(未満)では5×10^(-4)。
65°~68°(未満)では10×10^(-4)。
62°~65°(未満)では17×10^(-4)。
59°~62°(未満)では31×10^(-4)。
以上とし、やや厳密性を欠くがこの程度のやり方で
よい。この10^(0.25)ステップの数列、
1、3、5、10、17、31、56、・・・も覚
える必要がある。すなわち、
56°~59°(未満)では56×10^(-4)
になるとみられるが、60°以下だとかなり誤差が
増え、この方法は結果が悪くなる。
60°以上の場合の、sin(θ)の計算方法は上
の通り。
次に60°以下の場合は、
sin(θ°)(60°>θ°>0°)として
sin(θ°)=sin(15°刻みの中央)+{rad(1°)×sin(90°-15°刻みの中央)×10^4}×θ°×10^(-4)
とする。テーラー展開で、2次以下はばっさり切り
捨てて、1次までにした式を使うと言う意味である。
つまり、そのために{rad(1°)×sin(15°刻みの中央)×10^4}
の各々を、覚える必要が有ったのである。
ただし、以下が重要だが、上記の式は使わず、
sin(θ°)=sin(15°刻みの中央)+{rad(1°)×sin(90°-15°刻みの中央)×10^4}×(補正K)×θ°×10^(-4)
と、補正係数Kを加える
のである。
こうする事によって、2次以下を切り捨てた事に
よる弊害を防ぐという意味である。だから、結局の
所、ここで補正Kも、どうするのかを、覚える必要
がある。
起点sin(0°)の補正K=1(補正しない。)
起点sin(15°)の補正K:
15°以下を計算するマイナス計算のときK=1.02
15°以上を計算するプラス向計算のときK=0.98
起点sin(30°)の補正K:
30°以下を計算するマイナス計算のときK=1.04
30°以上を計算するプラス向計算のときK=0.96
起点sin(45°)の補正K:
45°以下を計算するマイナス計算のときK=1.07
45°以上を計算するプラス向計算のときK=0.93
起点sin(60°)の補正K:
60°以下を計算するマイナス計算のときK=1.12
60°以上を計算するプラス向計算のときK=0.89
なお、以下の数値は、誤差が大きく、実際には使えない。
起点sin(75°)の補正K:
75°以下を計算するマイナス計算のときK=1.23
60°以上を計算するプラス向計算のときK=0.81
つまり、K(下り)=1+0.02×1/15×(起点θ°)+0.01×(3.6)^{1/15×(起点θ°-45°)}、
K(上り)=1/K(下り)という式にほぼなっている。
以上の、補正はトライアンドエラーで出しているの
で、経験的なものでしかない。ようするに、書くと
ごちゃごちゃ表現されるが、折れ線で近似している
だけである。
説明は以上である。
例として、sin(10°)とsin(80°)
を求めてみる。”1/3角の法則”が有れば厳密解
が求まるケースではある。
sin(10°):
sin15°から出発する。
sin(10°)=sin(15°)-{rad(1°)×sin(75°)・・のデータ}×5×10^4×補正K(15°下り)
=0.2588-168.6×5×10^4×1.02
=0.17281(1回目)
sin(80°):
sin(80°)=1-rad(1°)×rad(1°)×1/2×10^4×100+補正項(80°・・77°以上)
=1-1.52×10^4×100+0.×10^4
=0.9848(結果・結論)
試しに、検算してみる。
0.17281×0.17281+0.9848×0.9848
=0.02986+0.96983=0.99969
0.00031だけ、誤差があり、このケースは
sin(10°)の補正係数(K)の誤差とみられる。
2×0.17281×δ(sin(10°)=0.00031
δ(sin(10°))=0.00090
よって、sin(10°)は、0.17281+0.00090
sin(10°)=0.17371(2回目・結果)
に近いと見られる。再度2乗和を取ると、
0.17371×0.17371+0.9848×0.9848
=0.03018+0.96983=1.00001。
実際に、集成万能数表(森北出版、森北常雄、1955)
を見てみると、
sin(10°)=0.1736482
sin(80°)=0.9848078
となっていて、sin(10°)第1回目の数値の
誤差には、計算方法の問題が少し有ったと見られる。
が、最終結果の残渣は概ね電卓の有効数字の問題で
あろうと、考える事が出来るだろう。(2020/06/24)
によらないゲームを考え、座標回転を議論している。通
常座標回転のsin(θ)cos(θ)は、関数電卓で
計算するのだが、ここでは簡便な筆算方法について考察
する。要旨から書く。sin(θ)を求めるとして、
60°から上と下とで分け、上は1-1/2θ^2方式
で、下は1+θ近似方式で求める。ただし、60°より
上については、最後に二次曲線から、はずれる部分を、
数値で微補正。
下については、傾きに係数を掛けて、折れ線近似で補
正してゆく。
では、以下に詳しく述べる。
まず、1°が0.0174533ラジアンである事、
つまりrad(1°)=0.0174533であり、
また次の数値は、覚える事にする。
sin(0°)=0.
sin(15°)=√6-√2/4=0.2588
sin(30°)=0.5000
sin(45°)=√2/2=0.7071
sin(60°)=√3/2=0.8660
sin(75°)=√6+√2/4=0.9659
sin(90°)=1
更に以下の数値を覚える事が、実際の計算では大切だ。
rad(1°)×sin(0°)×10^4=0
rad(1°)×sin(15°)×10^4=45.2
rad(1°)×sin(30°)×10^4=87.3
rad(1°)×sin(45°)×10^4=123.4
rad(1°)×sin(60°)×10^4=151.1
rad(1°)×sin(75°)×10^4=168.6
rad(1°)×sin(90°)×10^4=174.5
また、大事な定数は以下だ。
rad(1°)×rad(1°)×1/2×10^4=1.52
これらはこのケースは、座標回転の計算が実際に必
要なら、そのときには覚えるという覚悟を持てば、
使えるだろう。
まずは、座標を回転させる計算をするためには、
sin(θ)と、sin(90°-θ)を求める必
要がある。どちらの場合も、60°を境に上か下か
で、場合分けをする。
上の場合を先ず述べる。
sin(θ°)(90°>θ°>60°)として
sin(θ°)=sin(90°)-{rad(1°)×rad(1°)×1/2×10^4}×(θ°^2)×sin(90°)/10^4
=1-{rad(1°)×rad(1°)×1/2×10^4}×(θ°^2)/10^4
=1-1.52×(θ°^2)/10^4
これは、60°以上で、sin(θ)を90°を基
準に2次までテーラー展開しただけだ。当然90°
から離れると、かなりの誤差がある。それを、次の
ように補正する。
誤差がどの位かを、経験的に式で表す。つまり
誤差=-小数以下切捨て[10^{1/12*(78°-θ°)}]×10^(-4)
になると、考える。
だから、小数以下切捨て[10^{1/12*(78°-θ°)}]×10^(-4)
を足して補正する。ただし、90°から3°刻みで、
中心値で、代表させて良い。とどのつまり
小数以下切捨て[10^{1/12*(78°-θ°)}]×10^(-4)は、
θが77°以上では0×10^(-4)。
74°~77°(未満)では1×10^(-4)。
71°~74°(未満)では3×10^(-4)。
68°~71°(未満)では5×10^(-4)。
65°~68°(未満)では10×10^(-4)。
62°~65°(未満)では17×10^(-4)。
59°~62°(未満)では31×10^(-4)。
以上とし、やや厳密性を欠くがこの程度のやり方で
よい。この10^(0.25)ステップの数列、
1、3、5、10、17、31、56、・・・も覚
える必要がある。すなわち、
56°~59°(未満)では56×10^(-4)
になるとみられるが、60°以下だとかなり誤差が
増え、この方法は結果が悪くなる。
60°以上の場合の、sin(θ)の計算方法は上
の通り。
次に60°以下の場合は、
sin(θ°)(60°>θ°>0°)として
sin(θ°)=sin(15°刻みの中央)+{rad(1°)×sin(90°-15°刻みの中央)×10^4}×θ°×10^(-4)
とする。テーラー展開で、2次以下はばっさり切り
捨てて、1次までにした式を使うと言う意味である。
つまり、そのために{rad(1°)×sin(15°刻みの中央)×10^4}
の各々を、覚える必要が有ったのである。
ただし、以下が重要だが、上記の式は使わず、
sin(θ°)=sin(15°刻みの中央)+{rad(1°)×sin(90°-15°刻みの中央)×10^4}×(補正K)×θ°×10^(-4)
と、補正係数Kを加える
のである。
こうする事によって、2次以下を切り捨てた事に
よる弊害を防ぐという意味である。だから、結局の
所、ここで補正Kも、どうするのかを、覚える必要
がある。
起点sin(0°)の補正K=1(補正しない。)
起点sin(15°)の補正K:
15°以下を計算するマイナス計算のときK=1.02
15°以上を計算するプラス向計算のときK=0.98
起点sin(30°)の補正K:
30°以下を計算するマイナス計算のときK=1.04
30°以上を計算するプラス向計算のときK=0.96
起点sin(45°)の補正K:
45°以下を計算するマイナス計算のときK=1.07
45°以上を計算するプラス向計算のときK=0.93
起点sin(60°)の補正K:
60°以下を計算するマイナス計算のときK=1.12
60°以上を計算するプラス向計算のときK=0.89
なお、以下の数値は、誤差が大きく、実際には使えない。
起点sin(75°)の補正K:
75°以下を計算するマイナス計算のときK=1.23
60°以上を計算するプラス向計算のときK=0.81
つまり、K(下り)=1+0.02×1/15×(起点θ°)+0.01×(3.6)^{1/15×(起点θ°-45°)}、
K(上り)=1/K(下り)という式にほぼなっている。
以上の、補正はトライアンドエラーで出しているの
で、経験的なものでしかない。ようするに、書くと
ごちゃごちゃ表現されるが、折れ線で近似している
だけである。
説明は以上である。
例として、sin(10°)とsin(80°)
を求めてみる。”1/3角の法則”が有れば厳密解
が求まるケースではある。
sin(10°):
sin15°から出発する。
sin(10°)=sin(15°)-{rad(1°)×sin(75°)・・のデータ}×5×10^4×補正K(15°下り)
=0.2588-168.6×5×10^4×1.02
=0.17281(1回目)
sin(80°):
sin(80°)=1-rad(1°)×rad(1°)×1/2×10^4×100+補正項(80°・・77°以上)
=1-1.52×10^4×100+0.×10^4
=0.9848(結果・結論)
試しに、検算してみる。
0.17281×0.17281+0.9848×0.9848
=0.02986+0.96983=0.99969
0.00031だけ、誤差があり、このケースは
sin(10°)の補正係数(K)の誤差とみられる。
2×0.17281×δ(sin(10°)=0.00031
δ(sin(10°))=0.00090
よって、sin(10°)は、0.17281+0.00090
sin(10°)=0.17371(2回目・結果)
に近いと見られる。再度2乗和を取ると、
0.17371×0.17371+0.9848×0.9848
=0.03018+0.96983=1.00001。
実際に、集成万能数表(森北出版、森北常雄、1955)
を見てみると、
sin(10°)=0.1736482
sin(80°)=0.9848078
となっていて、sin(10°)第1回目の数値の
誤差には、計算方法の問題が少し有ったと見られる。
が、最終結果の残渣は概ね電卓の有効数字の問題で
あろうと、考える事が出来るだろう。(2020/06/24)
排除領域円でアナログ動ルール日本将棋に限界触問題(長さん)
以前に、ようするに日本将棋で、動きは0から
1歩まで自由、相手駒を取るのは升目の差し渡し
の7割半径の円に突入時で、1枚取ったらもう
取れない(今までの説明では、そこで止まる)
という、自然数歩みから実数歩歩み、ルールに座
標の取り方依存性無しという新作将棋について述
べた。暗算で、移動の座標変化を計算しながら指
す必要があるが、平方根の暗算が出来るようにな
れば、何とか指せるのではないかとの旨、述べて
きた。
今回は、新たに立ちはだかった壁について述べる。
深々と接触する相手駒とスレスレに接触する相手
駒の接触点までの距離が接近していて、しかも、
暗算なので有効数字が少ないときに、第1接触駒
を判定できない場合がある
という内容である。結論から言うと、直感的な第
2接触駒の接触点座標と、その第2接触駒の最接
近点座標の算術平均を取り、それより手前で、
直感的な第1限界接触駒が、
最接近点が0.7以下か、ないしはそれにかなり
近い距離で接触するカスリ接触のケースには、第
1限界接触駒を例外なく第1接触して、取り去る
駒にするという、補足ルールが必要
なようである。
なお以下では第1接触駒、ないしは第1限界接
触駒と表現する相手駒は、自駒走り経路直線に
一番近くでその最接近点となる相手駒の事であり、
第2接触駒等とは、より奥の方で走り経路直線へ
最接近する相手駒という意味にしよう。
では、説明を開始する。
簡単な場合で、第2接触駒が真っ芯に自駒とア
タる場合で、第1接触駒が横カスリ接触である
場合を以下の図のように考える。
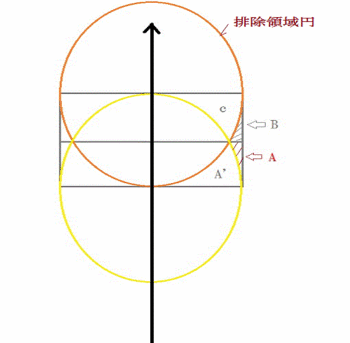
上図で、第1接触横カスリ駒は、茶色の円の中心
に有る、第2真っ芯接触相手駒の右側にあるとす
る。そもそも、
1)灰色の田の字領域以外では、第1接触駒は、
自駒に接触しない。
排除円、ここでは半径0.7升より、最接近点
が大きくなるからである。
次に、
2)第2接触相手駒の半径0.7以内の、茶色の
円の中に、第1接触相手駒は存在し得ない。
すると、2)の事から考慮が必要なのは、
A’、A、Bの3領域である事が判る。
そこで、
第2接触駒の自駒との接触点を中心に、
排除域半径(0.7)で図のように円を書くと、
3)A’のときには、第1接触カスリ駒が、
正常に第1接触し、Aのときに、第2接触駒から
の距離が遠いのに、
異常な逆転が起こる事が判る。
Bのときにも逆転が起こるが、第2接触駒との
距離差が接近してくるので、異常性は薄い。
Cの領域では、本来逆転するはずだが、第1接触
駒は第2接触駒の排除領域に入れないので、Cの
ような事は起こらない。
以上の事が判る。
そこで、Aの状態を問題にすると、
図形は縦横比が1:7前後で細長く、第1接触駒
の座標計算の精度に強く依存する。
従って、Aの領域の決定は、座標計算で平方根の
計算の有効数字が少ないと不確定的である。
だから、
異常な逆転は、無いものとするという、補足的な
ルールが必要である。
そこで補足ルールの一例としては、
4)このような第1接触駒が反対側から浅く接触
するケースには、真っ芯に近い第2接触駒の自駒
走行再接近点距離2乗と、接触点距離2乗の、
算術平均を取り、それより手前で第1浅接触駒が
接触する場合には、自駒走行直線との(最接近)
距離が0.7よりも概ね百分の1の桁で小さいと
いう計算になっても、0.7を越えなければ、
1位と2位の異常逆転は、起こらないというルー
ルを付け加える
という手が考えられた。
このように計算誤差がシビヤに効いてくるのは、
たとえば天文学で、限界線星食を利用して、月の
位置座標の精度を上げる
等、応用では御なじみのものである。つまり、
限界星食や限界掩蔽で、天体の位置精度が上がる
のだが。このケースは逆に、暗算の為、有効数字
が少ない事の粗が、出てしまうという意味である。
自然界ではレアーであるが、ゲームに於いては、
”相手の奥駒を取る手筋”として、常套手段とし
て、着手時選択される可能性が大きい。だから、
この点に関しての
ルールの取り方による局面への影響は、残念なが
ら、かなり大きいと予想される。
今述べた補足ルールは、数学的に完全とは期待
できないが、
無いよりマシで、付け加える必要が有りそうだ。
なお、今の説明では、第2接触駒が真っ芯の場
合を考えたが、すこし中心からズレル場合を考え
ると、以下の図のような感じになろう。
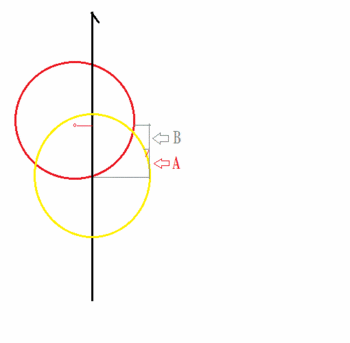
第2駒接触点距離2乗と、第2駒最接近点2乗
の算術平均は、第2駒接触点距離と、第2駒最接
近点距離の算術平均と、結果に大差は無いだろう。
この考えで、上の図のA領域の”反転”を、
例外的に無くしてしまえば、実際上は余り大きな
問題は、起こりにくいのではないか。
なお2次元のケースは、3駒競合は、現実的に
起こらないように私には見える。3次元ゲームで
は、更なる考察が必要だろう。
つまり将棋は2次元なので、たとえば、上の第
2接触駒への自駒の”突き刺し方”を、真っ芯か
ら外したケースで、第1接触駒と第2接触駒を同
じ側に持ってくると、接触逆転領域自体が、第2
接触駒の排除域飛び地のように、第2接触駒より
も遠い所に有るものの、今のルールで、切り捨て
られるので、問題が起こらない事がわかる。
従ってこの方法で実質的に、誤差による、着手
の合否の問題は、有る程度までは解決されると考
えられるのである。(2020/06/23)
1歩まで自由、相手駒を取るのは升目の差し渡し
の7割半径の円に突入時で、1枚取ったらもう
取れない(今までの説明では、そこで止まる)
という、自然数歩みから実数歩歩み、ルールに座
標の取り方依存性無しという新作将棋について述
べた。暗算で、移動の座標変化を計算しながら指
す必要があるが、平方根の暗算が出来るようにな
れば、何とか指せるのではないかとの旨、述べて
きた。
今回は、新たに立ちはだかった壁について述べる。
深々と接触する相手駒とスレスレに接触する相手
駒の接触点までの距離が接近していて、しかも、
暗算なので有効数字が少ないときに、第1接触駒
を判定できない場合がある
という内容である。結論から言うと、直感的な第
2接触駒の接触点座標と、その第2接触駒の最接
近点座標の算術平均を取り、それより手前で、
直感的な第1限界接触駒が、
最接近点が0.7以下か、ないしはそれにかなり
近い距離で接触するカスリ接触のケースには、第
1限界接触駒を例外なく第1接触して、取り去る
駒にするという、補足ルールが必要
なようである。
なお以下では第1接触駒、ないしは第1限界接
触駒と表現する相手駒は、自駒走り経路直線に
一番近くでその最接近点となる相手駒の事であり、
第2接触駒等とは、より奥の方で走り経路直線へ
最接近する相手駒という意味にしよう。
では、説明を開始する。
簡単な場合で、第2接触駒が真っ芯に自駒とア
タる場合で、第1接触駒が横カスリ接触である
場合を以下の図のように考える。

上図で、第1接触横カスリ駒は、茶色の円の中心
に有る、第2真っ芯接触相手駒の右側にあるとす
る。そもそも、
1)灰色の田の字領域以外では、第1接触駒は、
自駒に接触しない。
排除円、ここでは半径0.7升より、最接近点
が大きくなるからである。
次に、
2)第2接触相手駒の半径0.7以内の、茶色の
円の中に、第1接触相手駒は存在し得ない。
すると、2)の事から考慮が必要なのは、
A’、A、Bの3領域である事が判る。
そこで、
第2接触駒の自駒との接触点を中心に、
排除域半径(0.7)で図のように円を書くと、
3)A’のときには、第1接触カスリ駒が、
正常に第1接触し、Aのときに、第2接触駒から
の距離が遠いのに、
異常な逆転が起こる事が判る。
Bのときにも逆転が起こるが、第2接触駒との
距離差が接近してくるので、異常性は薄い。
Cの領域では、本来逆転するはずだが、第1接触
駒は第2接触駒の排除領域に入れないので、Cの
ような事は起こらない。
以上の事が判る。
そこで、Aの状態を問題にすると、
図形は縦横比が1:7前後で細長く、第1接触駒
の座標計算の精度に強く依存する。
従って、Aの領域の決定は、座標計算で平方根の
計算の有効数字が少ないと不確定的である。
だから、
異常な逆転は、無いものとするという、補足的な
ルールが必要である。
そこで補足ルールの一例としては、
4)このような第1接触駒が反対側から浅く接触
するケースには、真っ芯に近い第2接触駒の自駒
走行再接近点距離2乗と、接触点距離2乗の、
算術平均を取り、それより手前で第1浅接触駒が
接触する場合には、自駒走行直線との(最接近)
距離が0.7よりも概ね百分の1の桁で小さいと
いう計算になっても、0.7を越えなければ、
1位と2位の異常逆転は、起こらないというルー
ルを付け加える
という手が考えられた。
このように計算誤差がシビヤに効いてくるのは、
たとえば天文学で、限界線星食を利用して、月の
位置座標の精度を上げる
等、応用では御なじみのものである。つまり、
限界星食や限界掩蔽で、天体の位置精度が上がる
のだが。このケースは逆に、暗算の為、有効数字
が少ない事の粗が、出てしまうという意味である。
自然界ではレアーであるが、ゲームに於いては、
”相手の奥駒を取る手筋”として、常套手段とし
て、着手時選択される可能性が大きい。だから、
この点に関しての
ルールの取り方による局面への影響は、残念なが
ら、かなり大きいと予想される。
今述べた補足ルールは、数学的に完全とは期待
できないが、
無いよりマシで、付け加える必要が有りそうだ。
なお、今の説明では、第2接触駒が真っ芯の場
合を考えたが、すこし中心からズレル場合を考え
ると、以下の図のような感じになろう。

第2駒接触点距離2乗と、第2駒最接近点2乗
の算術平均は、第2駒接触点距離と、第2駒最接
近点距離の算術平均と、結果に大差は無いだろう。
この考えで、上の図のA領域の”反転”を、
例外的に無くしてしまえば、実際上は余り大きな
問題は、起こりにくいのではないか。
なお2次元のケースは、3駒競合は、現実的に
起こらないように私には見える。3次元ゲームで
は、更なる考察が必要だろう。
つまり将棋は2次元なので、たとえば、上の第
2接触駒への自駒の”突き刺し方”を、真っ芯か
ら外したケースで、第1接触駒と第2接触駒を同
じ側に持ってくると、接触逆転領域自体が、第2
接触駒の排除域飛び地のように、第2接触駒より
も遠い所に有るものの、今のルールで、切り捨て
られるので、問題が起こらない事がわかる。
従ってこの方法で実質的に、誤差による、着手
の合否の問題は、有る程度までは解決されると考
えられるのである。(2020/06/23)
富山市清水堂南遺跡不成銀将は双六盤と至近出土(長さん)
天童の将棋駒と全国遺跡出土駒(山形県天童市
・天童市将棋資料館・2001)2003年に、
以下に紹介の、発掘調査報告書も含めて記載さ
れているが、富山県富山市清水堂南遺跡の西暦
2001年前後に発掘された成り不明銀将駒は、
実は、
盤双六の盤と互いに1km弱の距離の範囲
内で、出土している
事が、以下の発掘報告書の85ページ付近で述
べられていた。
富山市埋蔵文化財調査報告113
富山市水橋金広・中馬場遺跡発掘報告書
2001年
富山市教育委員会。
上記発掘調査報告書は奈良文化財研究所の、
全国遺跡報告総覧のデータベース(urlは、
https://sitereports.nabunken.go.jp/ja)
の中にもある。pdfファイル名は、以下の通
りである。
13696_1_富山市水橋金広・中馬場遺跡発掘調査報告書.pdf
なお、将棋駒”成不明銀将”のスケッチが、
天童の将棋駒と全国遺跡出土駒の図と同じで、
”(参考)富山市清水堂南遺跡の銀将駒”とし
て、同報告書の、86ページ第50図にもある。
双六盤は、巻頭のカラー写真で同発掘報告書
に紹介され、本文中に出土状況、成立年代が、
16世紀中ごろから後半にかけて(安土桃山
時代頃)である事が記載されている。また厚盤
としては最初の発見であった旨が、同報告書の
84ページに、遊戯史学会理事、増川宏一氏名
で解説がある。成り不明銀将駒と共に、双六駒
と疑われる物品が、富山市清水堂南遺跡から
出土しており、増川宏一氏は”特定同一セット
の盤駒とは有る程度距離があり到底思えないが、
双六盤駒が同一地帯から出土した可能性が高い”
と論じている。言い忘れたが前記発掘報告書に
は、増川氏が指摘した、双六駒と疑われる物も、
スケッチがある。
この双六盤については、発掘された日本列島
等でも、紹介されていたように、私は記憶する。
地図を開けば判った事だったのかもしれない
が。従来より知られていた、富山市清水堂南遺
跡の銀将駒と、富山市水橋金広遺跡発掘の厚板
の双六盤は、成立時代がほぼ一緒でかつ、発掘
場所も、極端には離れておらず、更には将棋駒
といっしょに、双六駒が出土していた可能性が、
高いとの事のようである。
富山市市街が戦国時代以降にぎわっていた事は、
少なくとも確かだ。(2020/06/22)
・天童市将棋資料館・2001)2003年に、
以下に紹介の、発掘調査報告書も含めて記載さ
れているが、富山県富山市清水堂南遺跡の西暦
2001年前後に発掘された成り不明銀将駒は、
実は、
盤双六の盤と互いに1km弱の距離の範囲
内で、出土している
事が、以下の発掘報告書の85ページ付近で述
べられていた。
富山市埋蔵文化財調査報告113
富山市水橋金広・中馬場遺跡発掘報告書
2001年
富山市教育委員会。
上記発掘調査報告書は奈良文化財研究所の、
全国遺跡報告総覧のデータベース(urlは、
https://sitereports.nabunken.go.jp/ja)
の中にもある。pdfファイル名は、以下の通
りである。
13696_1_富山市水橋金広・中馬場遺跡発掘調査報告書.pdf
なお、将棋駒”成不明銀将”のスケッチが、
天童の将棋駒と全国遺跡出土駒の図と同じで、
”(参考)富山市清水堂南遺跡の銀将駒”とし
て、同報告書の、86ページ第50図にもある。
双六盤は、巻頭のカラー写真で同発掘報告書
に紹介され、本文中に出土状況、成立年代が、
16世紀中ごろから後半にかけて(安土桃山
時代頃)である事が記載されている。また厚盤
としては最初の発見であった旨が、同報告書の
84ページに、遊戯史学会理事、増川宏一氏名
で解説がある。成り不明銀将駒と共に、双六駒
と疑われる物品が、富山市清水堂南遺跡から
出土しており、増川宏一氏は”特定同一セット
の盤駒とは有る程度距離があり到底思えないが、
双六盤駒が同一地帯から出土した可能性が高い”
と論じている。言い忘れたが前記発掘報告書に
は、増川氏が指摘した、双六駒と疑われる物も、
スケッチがある。
この双六盤については、発掘された日本列島
等でも、紹介されていたように、私は記憶する。
地図を開けば判った事だったのかもしれない
が。従来より知られていた、富山市清水堂南遺
跡の銀将駒と、富山市水橋金広遺跡発掘の厚板
の双六盤は、成立時代がほぼ一緒でかつ、発掘
場所も、極端には離れておらず、更には将棋駒
といっしょに、双六駒が出土していた可能性が、
高いとの事のようである。
富山市市街が戦国時代以降にぎわっていた事は、
少なくとも確かだ。(2020/06/22)







