飛車型と角行型の2種の実数動将棋停止点計算は簡単(長さん)
以前に述べた通り、実数歩みや走りのできる
日本将棋をするとして、相手の駒を取った場合
の停止点を、排除円表面とする場合、元の相手
駒位置に移動する場合等に比べて、
暗算での移動先座標計算がより煩雑になる。
前回までの説明では、かなり煩雑な手順で、
座標計算を実際にして来た。しかしその後、
縦横と斜めという、飛車と角行型つまり、
(0°、90°、180°、270°)型と、
(45°、135°、225°、315°)型
の事実上、2種類の動きしかない、日本将棋で
は、
以前述べた方法に比べて、著しく簡単に座標を
出す方法があるのに気がついた
ので、今回はそれについて述べる。
つまり、
(45°、135°、225°、315°)型
は45°座標回転する計算は1/√2を係数に
しながらすれば簡単。結局飛車型の座標計算で
済むというものである。更に合わせて、2個
の相手駒のうち、手前のカスリ駒が、奥の真正
面衝突駒に比べて、かなり近い場合は、逆転を
認めない例外規則に於いて、日本将棋では、
基準を二乗距離の中央ではなくて、単純に距離
の平均としてよいとの
旨、以前の本ブログで述べた試論を訂正する。
では、説明を開始する。
以前の論では、一般的な角度での走りを考え
たため、最接近点までの距離の2乗を求めてか
ら、平方根を取らずに、排除円に到達するまで
の、距離の2乗を計算するという、
厳格だが、煩雑な計算が必要
だった。しかし考えてみれば、
香車走りのときには、最接近点の座標は、取り
去る相手駒の段数に等しい点までの、元の位置
からの距離の事でしかない。
更には、
相手駒の走り直線からの最接近距離は、筋の違
いの歩数でしかない。
つまり(0°、90°、180°、270°)型
の場合には、最接近点までの距離は簡単に出る
ので、その2乗値は、考える必要そのものが元々
無い。
せいぜい、√(0.49-最接近距離2乗)の、
更に√開きに当る平方根計算をして、自駒の停
止点を、その分手前に置く計算を1度するだけ
である。
そこで、次に(45°、135°、225°、
315°)型の角行動きの場合を考えると、
45°+n×90°の座標の回転は、符号は、
適宜盤面から判断するとして絶対値については、
Y座標を(x+y)/√2、
X座標を(x-y)/√2にして、
Y座標が再接近点距離を表し、X座標が相手駒
から走り経路までの垂線距離になるだけ
だったのである。つまり、45°+n×90°
の座標の回転では、sin(45°)=
cos(45°)=1/√2なので、積極的に
座標回転をした方が、計算がむしろ楽になる。
ここで、そうしてから、衝突が起こる排除円
の分だけ、座標を前にズラすのであるが、
そのとき0.7が0.99/√2と事実上等し
い事が使える。0.7の2乗も0.98/2だ
として、45°計算の場合は計算し、続ければ
良いだけだ。後で√をとると、/2は再び、
/√2に戻る。
つまり、手前にシフトさせる計算をするときに、
最後まで1/√2を、共通係数として残す事も、
さほど難しくなかったのである。
最後に元の座標に戻すために、もう一度、
45°+n×90°の座標の回転をする必要が
あるが、このとき、/√2は/2になって、
答えを1/2するだけになり、×0.7071
の4桁掛け算計算等は無い。
繰り返すが盤面が読めれば絶対値を取って座
標回転計算をすれば良く、戻すときに符号を元
戻しすれば良いだけである。つまり重要な点は、
角行動きの45°斜め動きの座標計算の場合は、
たまたまだったのだが、
sin(45°)もcos(45°)も1/√2
でしかないので、数桁の掛け算とか、足し引き
という、1桁の掛け算・割り算、2桁の足し引
き算よりも、めんどくさいような掛け算、足し
引き算は、元々出てこないという事
が有ったのである。
一例として駒を取ったため、0.3歩進んだ
(0.5、0.8)に居る駒を、後方から角行
動きで、向こう升目で相手が再度取り返すが、
本来は筋違いで、1升目深く入り込んで取る場
合の座標計算をしてみる。それは今述べた方法
だと、次のようになる。
(-5.5、-5.5)の位置に、元々の角行
が居るとして、斜めに6歩角行が戻ると、
(0.5,0.5)点を通過する。つまり、
(0.5+0.3/2、0.5+0.3/2)
の点が、最接近点である。
つまり45°走りのとき、最接近点座標が、
現実には比較的簡単に判るという点がポイント。
しかしこの最接近点座標の計算が、具体的に
どうなるのか、慣れないと残念ながら、少し
紛れやすい。しかし45°走り型のときには、
図示すると明白なので、ワンパターンだとして、
このパターンに関しては、記憶した方が良い。
なお0.8-0.5=0.3だ。
そこで原点で座標回転すると、最接近点で、
角行が(0、(1+0.6/2)/√2)、
自駒が(0.3/√2、1.3/√2)となり、
Y座標同士が、確かに一致している。そして
√(0.99/√2)^2-(0.3/√2)^2
√(0.89/2)≒0.94/√2となる。
√2は、最後まで残しておく。つまり、相手
角行の移動先座標は、
(0、(1-0.94+0.3)/√2)=
(0、0.36/√2)である。
そしてまた、45°+n×90°座標回転し
て、よって角行の座標は、
(0.18、0.18)
となり、中央点を0とみれば0.32升だけ、
升目中央から段・筋ともに角行はズレた入り込
位置に移動する事が判る。この計算はルート計
算が、0.89のルートしか無いので、近似的
な計算を暗算でするのが容易である。他の
(0.5、0.8)型駒取りについての計算な
ら、似たようなもののはずである。
明らかに慣れれば、今度は暗算が容易だ。
最後に、冒頭の結論で述べた、2つの相手駒
のうちの、どちらを捕獲するのかという問題に
ついて、以前の議論を訂正する。
すなわち、以上の計算から見て明らかなよう
に、高々角行動きしか無い日本将棋のケースに
は、最接近点までの自駒移動距離に関して、
2乗距離を考える事が無い。そこで、以前述べ
た下のような図のケースで、
p12点をp1点距離とp2点距離の単純平均
ではなくて、p1点距離の2乗とp2点距離の
2乗の平均にしなければならない理由は無い。
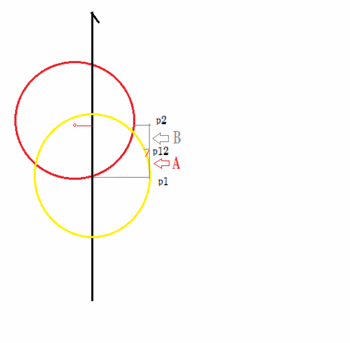
つまり、座標計算精度が√計算の所で落ちるた
めに、カスリ駒に関する衝突順位の反転の例外
を無くす特例に関しては、単に
奥駒の衝突点、最接近点の、位置の平均点を例
外ルール境目の基準にすれば良いというだけだ
という事になると見られるのである。(2020/07/13)
日本将棋をするとして、相手の駒を取った場合
の停止点を、排除円表面とする場合、元の相手
駒位置に移動する場合等に比べて、
暗算での移動先座標計算がより煩雑になる。
前回までの説明では、かなり煩雑な手順で、
座標計算を実際にして来た。しかしその後、
縦横と斜めという、飛車と角行型つまり、
(0°、90°、180°、270°)型と、
(45°、135°、225°、315°)型
の事実上、2種類の動きしかない、日本将棋で
は、
以前述べた方法に比べて、著しく簡単に座標を
出す方法があるのに気がついた
ので、今回はそれについて述べる。
つまり、
(45°、135°、225°、315°)型
は45°座標回転する計算は1/√2を係数に
しながらすれば簡単。結局飛車型の座標計算で
済むというものである。更に合わせて、2個
の相手駒のうち、手前のカスリ駒が、奥の真正
面衝突駒に比べて、かなり近い場合は、逆転を
認めない例外規則に於いて、日本将棋では、
基準を二乗距離の中央ではなくて、単純に距離
の平均としてよいとの
旨、以前の本ブログで述べた試論を訂正する。
では、説明を開始する。
以前の論では、一般的な角度での走りを考え
たため、最接近点までの距離の2乗を求めてか
ら、平方根を取らずに、排除円に到達するまで
の、距離の2乗を計算するという、
厳格だが、煩雑な計算が必要
だった。しかし考えてみれば、
香車走りのときには、最接近点の座標は、取り
去る相手駒の段数に等しい点までの、元の位置
からの距離の事でしかない。
更には、
相手駒の走り直線からの最接近距離は、筋の違
いの歩数でしかない。
つまり(0°、90°、180°、270°)型
の場合には、最接近点までの距離は簡単に出る
ので、その2乗値は、考える必要そのものが元々
無い。
せいぜい、√(0.49-最接近距離2乗)の、
更に√開きに当る平方根計算をして、自駒の停
止点を、その分手前に置く計算を1度するだけ
である。
そこで、次に(45°、135°、225°、
315°)型の角行動きの場合を考えると、
45°+n×90°の座標の回転は、符号は、
適宜盤面から判断するとして絶対値については、
Y座標を(x+y)/√2、
X座標を(x-y)/√2にして、
Y座標が再接近点距離を表し、X座標が相手駒
から走り経路までの垂線距離になるだけ
だったのである。つまり、45°+n×90°
の座標の回転では、sin(45°)=
cos(45°)=1/√2なので、積極的に
座標回転をした方が、計算がむしろ楽になる。
ここで、そうしてから、衝突が起こる排除円
の分だけ、座標を前にズラすのであるが、
そのとき0.7が0.99/√2と事実上等し
い事が使える。0.7の2乗も0.98/2だ
として、45°計算の場合は計算し、続ければ
良いだけだ。後で√をとると、/2は再び、
/√2に戻る。
つまり、手前にシフトさせる計算をするときに、
最後まで1/√2を、共通係数として残す事も、
さほど難しくなかったのである。
最後に元の座標に戻すために、もう一度、
45°+n×90°の座標の回転をする必要が
あるが、このとき、/√2は/2になって、
答えを1/2するだけになり、×0.7071
の4桁掛け算計算等は無い。
繰り返すが盤面が読めれば絶対値を取って座
標回転計算をすれば良く、戻すときに符号を元
戻しすれば良いだけである。つまり重要な点は、
角行動きの45°斜め動きの座標計算の場合は、
たまたまだったのだが、
sin(45°)もcos(45°)も1/√2
でしかないので、数桁の掛け算とか、足し引き
という、1桁の掛け算・割り算、2桁の足し引
き算よりも、めんどくさいような掛け算、足し
引き算は、元々出てこないという事
が有ったのである。
一例として駒を取ったため、0.3歩進んだ
(0.5、0.8)に居る駒を、後方から角行
動きで、向こう升目で相手が再度取り返すが、
本来は筋違いで、1升目深く入り込んで取る場
合の座標計算をしてみる。それは今述べた方法
だと、次のようになる。
(-5.5、-5.5)の位置に、元々の角行
が居るとして、斜めに6歩角行が戻ると、
(0.5,0.5)点を通過する。つまり、
(0.5+0.3/2、0.5+0.3/2)
の点が、最接近点である。
つまり45°走りのとき、最接近点座標が、
現実には比較的簡単に判るという点がポイント。
しかしこの最接近点座標の計算が、具体的に
どうなるのか、慣れないと残念ながら、少し
紛れやすい。しかし45°走り型のときには、
図示すると明白なので、ワンパターンだとして、
このパターンに関しては、記憶した方が良い。
なお0.8-0.5=0.3だ。
そこで原点で座標回転すると、最接近点で、
角行が(0、(1+0.6/2)/√2)、
自駒が(0.3/√2、1.3/√2)となり、
Y座標同士が、確かに一致している。そして
√(0.99/√2)^2-(0.3/√2)^2
√(0.89/2)≒0.94/√2となる。
√2は、最後まで残しておく。つまり、相手
角行の移動先座標は、
(0、(1-0.94+0.3)/√2)=
(0、0.36/√2)である。
そしてまた、45°+n×90°座標回転し
て、よって角行の座標は、
(0.18、0.18)
となり、中央点を0とみれば0.32升だけ、
升目中央から段・筋ともに角行はズレた入り込
位置に移動する事が判る。この計算はルート計
算が、0.89のルートしか無いので、近似的
な計算を暗算でするのが容易である。他の
(0.5、0.8)型駒取りについての計算な
ら、似たようなもののはずである。
明らかに慣れれば、今度は暗算が容易だ。
最後に、冒頭の結論で述べた、2つの相手駒
のうちの、どちらを捕獲するのかという問題に
ついて、以前の議論を訂正する。
すなわち、以上の計算から見て明らかなよう
に、高々角行動きしか無い日本将棋のケースに
は、最接近点までの自駒移動距離に関して、
2乗距離を考える事が無い。そこで、以前述べ
た下のような図のケースで、
p12点をp1点距離とp2点距離の単純平均
ではなくて、p1点距離の2乗とp2点距離の
2乗の平均にしなければならない理由は無い。

つまり、座標計算精度が√計算の所で落ちるた
めに、カスリ駒に関する衝突順位の反転の例外
を無くす特例に関しては、単に
奥駒の衝突点、最接近点の、位置の平均点を例
外ルール境目の基準にすれば良いというだけだ
という事になると見られるのである。(2020/07/13)







