二円共通内接線計算に暗算困難な例存在(長さん)
今迄述べたように、幾何学で同半径の2円の
共通内接線のY切片値を、暗算で正確に求め
る演算は、さほど困難では無い例がある。
しかしながら今回は、方位角を求めて比較
するほうが、はるかに楽な例が見つかったの
で、以下に報告する。
2の0と6の3で8の3の駒を被覆可能、
または、方位角を45°以上にしてY切片
精度を出すため同じ計算になるのだが、
0の2と3の6で3の8の駒を被覆可能かを、
升目に対して1/√2半径の排除円(前記
被覆円)2円について調べる演算である。
一例では自陣左香車の位置に超奔王を置き、
味方の左香車上の初期位置歩兵と、相手の
右辺金将先の初期位置歩兵で、相手初期位置
右金将が隠れるのかという、たまに起こるか
もしれないようにも見えるケースである。以
下の結果から、着手すると禁手負けになるが、
以前、三角関数表やPCを使った正確な計算
と、円の視半径42°を定数として円視半径
升目距離逆比例暗算の近似計算とで、非合法
手になるとの結論に、差が無い事も確かめて
いる。
最初に、方位角を45°以下にする最初の
パターンで、以前求めたように、計算すると、
2の0駒については三角関数厳密計算で上が、
20.705°。6の3駒が、三角関数厳密
計算で下が、20.514°に近くなるのだ
が、略算でどうなるのかを、確かめてみる。
なお、パソコンでN88Basicを使って
出したリストの、35番と36番のケースで
ある。
既に示したが、2の0駒の視半径は21°
であり、方位角は中心0°で上限21.0°。
6の3駒は視半径が18.7829/3≒
6.261°で、方位角が42×(1/2)
+5.5で26.5°と略算するから下限は、
20.239°で、非合法だと略算で簡単に
出る。
そこで、今度は幾何学で共通内接線を求め
て、Y切片が負で非合法と出るのかどうかを
確かめてみる。
今度は、Y切片の精度を出すため、同じ計
算だが0の2と3の6で3の8の駒を被覆可
能かどうか、後の問題に形式的に直してから
調べる演算をする。
ごちゃごちゃするが、下図のようになる。

つまり、0の2と3の6の円の中心を結ん
だ線が、水平になるように回転しておいて、
共通内接線の正接(傾き)を上図のように
計算すると、√(2/23)になるようで
ある。
そこで、三角関数の正接の加法定理の式に
代入すると、上図にも書いたが、
(4/3)+√(2/23)/
1-(4/3)×√(2/23)
となるのだが、有理化するために分母分子に
1+(4/3)×√(2/23)を掛けて
展開したとき、分母が175/207になる
等で、余り暗算が楽では無い。
結局 大学入試の回答風に書くと、正接の合
成で得られる2円共通内接線の傾きは
(12+√46)/7になるようだが、
Y切片が0のときの傾き:4/1.5と比較
するには、(36+√414)/21に通分
し、複雑化し直す必要がある。
つまり、
(36+√414)/21>(36+√400)/21
=56/21=4/1.5
を使いY切片は負になると計算するのである。
両計算とも、着手は非合法でこのケースは一
致するのだが、このように、
方位角を略算した方が、はるかに速いケース
が有る
のである。よって、本ブログで発案した奔将
棋の超奔王ルールでは、2つの駒の隙間から、
取りたい駒が超奔王駒から見て、ほんの一部
でも良いから見えているのかどうかという、
円の共通内接線の方程式を求めるパターンの
計算では、
最初に示した、方位角略算を優先させるよう
なルールに、やはりした方が良い
と私は今回ようやく、はっきりと認識出来た。
たぶん、ピタゴラスの3角形に2円の共通
内接線型になる2円の傾きやY切片問題の中
に、有理化で16×2/(9×23)という
ような分数が出来て、消去出来ないような、
余り面白くない例が有るという事までは、各
種大学受験問題集にも、載って無いのではな
いかと、私は予想している。何故なら、それ
を受験生にさせる事に対するフォークソング
の、昔の「受験生ブルース」の文句にあるよ
うな反感を、彼らに抱かせないようにする為、
避ける為であると、本ブログの管理人は邪推
するからである。(2023/11/10)
共通内接線のY切片値を、暗算で正確に求め
る演算は、さほど困難では無い例がある。
しかしながら今回は、方位角を求めて比較
するほうが、はるかに楽な例が見つかったの
で、以下に報告する。
2の0と6の3で8の3の駒を被覆可能、
または、方位角を45°以上にしてY切片
精度を出すため同じ計算になるのだが、
0の2と3の6で3の8の駒を被覆可能かを、
升目に対して1/√2半径の排除円(前記
被覆円)2円について調べる演算である。
一例では自陣左香車の位置に超奔王を置き、
味方の左香車上の初期位置歩兵と、相手の
右辺金将先の初期位置歩兵で、相手初期位置
右金将が隠れるのかという、たまに起こるか
もしれないようにも見えるケースである。以
下の結果から、着手すると禁手負けになるが、
以前、三角関数表やPCを使った正確な計算
と、円の視半径42°を定数として円視半径
升目距離逆比例暗算の近似計算とで、非合法
手になるとの結論に、差が無い事も確かめて
いる。
最初に、方位角を45°以下にする最初の
パターンで、以前求めたように、計算すると、
2の0駒については三角関数厳密計算で上が、
20.705°。6の3駒が、三角関数厳密
計算で下が、20.514°に近くなるのだ
が、略算でどうなるのかを、確かめてみる。
なお、パソコンでN88Basicを使って
出したリストの、35番と36番のケースで
ある。
既に示したが、2の0駒の視半径は21°
であり、方位角は中心0°で上限21.0°。
6の3駒は視半径が18.7829/3≒
6.261°で、方位角が42×(1/2)
+5.5で26.5°と略算するから下限は、
20.239°で、非合法だと略算で簡単に
出る。
そこで、今度は幾何学で共通内接線を求め
て、Y切片が負で非合法と出るのかどうかを
確かめてみる。
今度は、Y切片の精度を出すため、同じ計
算だが0の2と3の6で3の8の駒を被覆可
能かどうか、後の問題に形式的に直してから
調べる演算をする。
ごちゃごちゃするが、下図のようになる。

つまり、0の2と3の6の円の中心を結ん
だ線が、水平になるように回転しておいて、
共通内接線の正接(傾き)を上図のように
計算すると、√(2/23)になるようで
ある。
そこで、三角関数の正接の加法定理の式に
代入すると、上図にも書いたが、
(4/3)+√(2/23)/
1-(4/3)×√(2/23)
となるのだが、有理化するために分母分子に
1+(4/3)×√(2/23)を掛けて
展開したとき、分母が175/207になる
等で、余り暗算が楽では無い。
結局 大学入試の回答風に書くと、正接の合
成で得られる2円共通内接線の傾きは
(12+√46)/7になるようだが、
Y切片が0のときの傾き:4/1.5と比較
するには、(36+√414)/21に通分
し、複雑化し直す必要がある。
つまり、
(36+√414)/21>(36+√400)/21
=56/21=4/1.5
を使いY切片は負になると計算するのである。
両計算とも、着手は非合法でこのケースは一
致するのだが、このように、
方位角を略算した方が、はるかに速いケース
が有る
のである。よって、本ブログで発案した奔将
棋の超奔王ルールでは、2つの駒の隙間から、
取りたい駒が超奔王駒から見て、ほんの一部
でも良いから見えているのかどうかという、
円の共通内接線の方程式を求めるパターンの
計算では、
最初に示した、方位角略算を優先させるよう
なルールに、やはりした方が良い
と私は今回ようやく、はっきりと認識出来た。
たぶん、ピタゴラスの3角形に2円の共通
内接線型になる2円の傾きやY切片問題の中
に、有理化で16×2/(9×23)という
ような分数が出来て、消去出来ないような、
余り面白くない例が有るという事までは、各
種大学受験問題集にも、載って無いのではな
いかと、私は予想している。何故なら、それ
を受験生にさせる事に対するフォークソング
の、昔の「受験生ブルース」の文句にあるよ
うな反感を、彼らに抱かせないようにする為、
避ける為であると、本ブログの管理人は邪推
するからである。(2023/11/10)
超奔王の着手合否判断。簡易方位角法過誤ケース残り2つ(長さん)
直近、途中駒1の4と途中駒3の5のケースについて、
それ以遠の3の7の駒を完全に隠すかどうか、一例では、
0の0が▲5八位置だったとして、3の7の▲2一桂馬
が▲4四歩兵と△2三歩兵の存在下で初期▲5八位置
超奔王で直射するのかという問題を、2円の共通内接線
の幾何学を使ったY切片計算で判断する例を示した。
簡易方位角法で、厳密な角度の順序が逆転する4例の
うちの一つであった。このうち他の例であるが、2駒の
隙間が、無限小になる(0の5)と(1の2)の間の穴
の有無の場合も、別の記事で示している。
今回は今述べた2例同様、超奔王が途中2駒の間を突
き抜けて、向こうの駒を取れるかどうかを判定する手法
で、簡易方位角計算では逆転する、残りの2例について、
幾何学でY切片の符号から、厳密に判断する計算をした
ので、以下に結果を、1の4と3の5で、3の7駒が
取れるかどうかの問題と同様に、計算の過程について説
明する。
まず、0の4と2の7が有っても、0の0から2の8
の駒が超奔王には直射しているのかどうかという問題が
ある。厳密計算で、合法(穴有り/突き抜ける)を説明
する。この例は、超奔王を自陣最下段に落として相手陣
最奥を攻める手で、実戦では余り現れ難いとみられる。
以下の図のように、途中駒を水平に寝かせると、共通
接線の傾きは、√(2/11)になる。
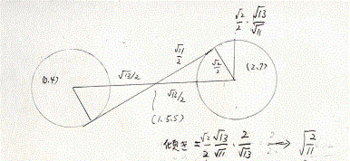
そこで三角関数の正接の加法定理の式は次のようになる。
(3/2)+√(2/11)/1-{(3/2)×√(2/11)}
分子分母に、1+{(3/2)×√(2/11)}を掛け
て、通常通り有理化する。
分子=(3/2)+√(2/11)+(9/4)×√(2/11)+(3/2)×(2×11)
=(3/2)×(13/11)+(13/4)√(2/11)
分母=1-(9/4)×(2/11)=13/22
より、最初の式は
=(22/13)×{(3/2)×(13/11)+(13/4)√(2/11)}
=3+(11/2)×√(2/11)=3+(11/2)×√(2×11)/11
=3+√22/2<3+√25/2=3+2.5=5.5
となり、X=0でY切片はプラスになるから合法である。
こちらは、√22<√25を使うので、直近で示した、
途中駒1の4と途中駒3の5のケースと同じような感じ
で、この0の4と2の7駒のケースは証明の調子が良い。
次は、0の0から見て、4の3位置駒と7の3位置駒
で8の4の駒を隠すかどうか。つまり例えば自陣右香車
初期位置0の0の超奔王から見て8の4位置の初期位置
の相手玉将の直射が、自陣右金前中段位置の4の3位置
の歩兵と、相手元の左金前に置かれた、7の3位置の、
相手の防御駒で例えば、邪魔になるかどうかという、こ
ちらも簡易方位角計算で、「非合法」への逆転例である。
このケースも自陣最下段位置から、相手陣最奥を超奔王
で攻める局面が、実戦では出難いので、現れる頻度は、
比較的レアーとみられる。
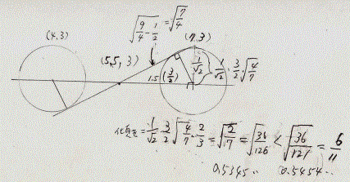
こちらは、上図中に傾き計算を入れた。間途中2駒が、
元々水平配置で傾き0なので、共通内接線の傾きだけで、
Y切片の傾きが決まる、特殊なケースである。
傾きが3/5.5以下なら合法なのだが、答えが
√(2/7)と出て本ブログの管理人などは3/5.5
と比較をどうしようかと、焦りを引き起こす。一応上図
でネタバレにしてしまったが、3/5.5は分子分母を
2倍にしてから、平方根表現に直す。つまり√記号の中
に2乗して数値を入れる。
他方、√(2/7)には、いま”2乗化”で求めた
√(36/121)となるY切片0となる場合の傾き値
に合わせる目的で、
(2/7)の分子・分母に√18を掛け√(36/126)
にする。
そうすると、このケースは分子では無く
分母同士の比較で大小が判る。
つまり、計算のめんどうさでは無くて、
どうしたら良いのか気がつくのに、手間が掛かる
という点で、方位角比較に比べて、楽かどうかが謎にな
るという例に、たまたまなっているようである。
この例に関しては、
y切片符号自体の計算が、かなり楽なので、0になる場
合との傾き値の比較方法で、考え込む時間が幾らか有っ
ても、それを出すまでの計算の簡単さが救いになる例
だろう。
以上から「『途中2駒から、第3のターゲット駒が、
取れるかどうか』の合否は、方位角比較方法によるが、
幾何学的に厳密解が出せる場合は、そちらを優先する」
という以前の提案のような表現にするしか、今の所無い。
そしてそのようにして、
玉虫色のルールで行くしか無く、後半に示した最後の比
較でつまづく例が、どの程度有るかは良く判らない。
ので、いまのところルールがこれで、問題が皆無かどう
かも実際は微妙で、個人的に私にはよく判らない。棋士
の数学能力を、現実に調査し無いと判らないほど曖昧で
あると結論出来る。以上のように本ブログの管理人には、
認識された。(2023/11/09)
それ以遠の3の7の駒を完全に隠すかどうか、一例では、
0の0が▲5八位置だったとして、3の7の▲2一桂馬
が▲4四歩兵と△2三歩兵の存在下で初期▲5八位置
超奔王で直射するのかという問題を、2円の共通内接線
の幾何学を使ったY切片計算で判断する例を示した。
簡易方位角法で、厳密な角度の順序が逆転する4例の
うちの一つであった。このうち他の例であるが、2駒の
隙間が、無限小になる(0の5)と(1の2)の間の穴
の有無の場合も、別の記事で示している。
今回は今述べた2例同様、超奔王が途中2駒の間を突
き抜けて、向こうの駒を取れるかどうかを判定する手法
で、簡易方位角計算では逆転する、残りの2例について、
幾何学でY切片の符号から、厳密に判断する計算をした
ので、以下に結果を、1の4と3の5で、3の7駒が
取れるかどうかの問題と同様に、計算の過程について説
明する。
まず、0の4と2の7が有っても、0の0から2の8
の駒が超奔王には直射しているのかどうかという問題が
ある。厳密計算で、合法(穴有り/突き抜ける)を説明
する。この例は、超奔王を自陣最下段に落として相手陣
最奥を攻める手で、実戦では余り現れ難いとみられる。
以下の図のように、途中駒を水平に寝かせると、共通
接線の傾きは、√(2/11)になる。
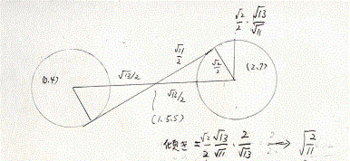
そこで三角関数の正接の加法定理の式は次のようになる。
(3/2)+√(2/11)/1-{(3/2)×√(2/11)}
分子分母に、1+{(3/2)×√(2/11)}を掛け
て、通常通り有理化する。
分子=(3/2)+√(2/11)+(9/4)×√(2/11)+(3/2)×(2×11)
=(3/2)×(13/11)+(13/4)√(2/11)
分母=1-(9/4)×(2/11)=13/22
より、最初の式は
=(22/13)×{(3/2)×(13/11)+(13/4)√(2/11)}
=3+(11/2)×√(2/11)=3+(11/2)×√(2×11)/11
=3+√22/2<3+√25/2=3+2.5=5.5
となり、X=0でY切片はプラスになるから合法である。
こちらは、√22<√25を使うので、直近で示した、
途中駒1の4と途中駒3の5のケースと同じような感じ
で、この0の4と2の7駒のケースは証明の調子が良い。
次は、0の0から見て、4の3位置駒と7の3位置駒
で8の4の駒を隠すかどうか。つまり例えば自陣右香車
初期位置0の0の超奔王から見て8の4位置の初期位置
の相手玉将の直射が、自陣右金前中段位置の4の3位置
の歩兵と、相手元の左金前に置かれた、7の3位置の、
相手の防御駒で例えば、邪魔になるかどうかという、こ
ちらも簡易方位角計算で、「非合法」への逆転例である。
このケースも自陣最下段位置から、相手陣最奥を超奔王
で攻める局面が、実戦では出難いので、現れる頻度は、
比較的レアーとみられる。
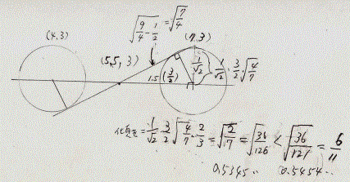
こちらは、上図中に傾き計算を入れた。間途中2駒が、
元々水平配置で傾き0なので、共通内接線の傾きだけで、
Y切片の傾きが決まる、特殊なケースである。
傾きが3/5.5以下なら合法なのだが、答えが
√(2/7)と出て本ブログの管理人などは3/5.5
と比較をどうしようかと、焦りを引き起こす。一応上図
でネタバレにしてしまったが、3/5.5は分子分母を
2倍にしてから、平方根表現に直す。つまり√記号の中
に2乗して数値を入れる。
他方、√(2/7)には、いま”2乗化”で求めた
√(36/121)となるY切片0となる場合の傾き値
に合わせる目的で、
(2/7)の分子・分母に√18を掛け√(36/126)
にする。
そうすると、このケースは分子では無く
分母同士の比較で大小が判る。
つまり、計算のめんどうさでは無くて、
どうしたら良いのか気がつくのに、手間が掛かる
という点で、方位角比較に比べて、楽かどうかが謎にな
るという例に、たまたまなっているようである。
この例に関しては、
y切片符号自体の計算が、かなり楽なので、0になる場
合との傾き値の比較方法で、考え込む時間が幾らか有っ
ても、それを出すまでの計算の簡単さが救いになる例
だろう。
以上から「『途中2駒から、第3のターゲット駒が、
取れるかどうか』の合否は、方位角比較方法によるが、
幾何学的に厳密解が出せる場合は、そちらを優先する」
という以前の提案のような表現にするしか、今の所無い。
そしてそのようにして、
玉虫色のルールで行くしか無く、後半に示した最後の比
較でつまづく例が、どの程度有るかは良く判らない。
ので、いまのところルールがこれで、問題が皆無かどう
かも実際は微妙で、個人的に私にはよく判らない。棋士
の数学能力を、現実に調査し無いと判らないほど曖昧で
あると結論出来る。以上のように本ブログの管理人には、
認識された。(2023/11/09)
1/2+√(2/3)/{1-1/2×√(2/3)}は有理化で1+√6/2(長さん)
「表題の式の値は1.3164965/0.5917517
の暗算で頓挫」と、以前に述べた件の続きである。
普通に有理化すると、
1+√6/2<1+√6.25/2=2.25で、
4.5-2×2.25=0よりは大きいので、
y切片はプラスで、合法手になるようだ。
とんでもない大ボケを記事にしてしまったものだ。
一応詳しく書くと、以下のようになる。
{1/2+√(2/3)}/{1-1/2×√(2/3)}=
1/2{1+2√(2/3)}/{1-1/2×√(2/3)}=
ここから、普通に有理化すると、
1/2{1+2√(2/3)}{1+1/2×√(2/3)}/
〔{1-1/2×√(2/3)}{1+1/2×√(2/3)}〕=
1/2{1+2√(2/3)}{1+1/2×√(2/3)}/
〔1-1/4×(2/3)〕=
1/2{1+2√(2/3)}{1+1/2×√(2/3)}/
〔5/6〕=
3/5{1+2√(2/3)}{1+1/2×√(2/3)}=
3/5〔1+{2√(2/3)}+{1/2×√(2/3)}+{2/3}〕=
3/5〔1+{5/2×√(2/3)}+{2/3}〕=
3/5〔5/3+{5/2×√(2/3)}〕=
1+3/2×√(2/3)=1+〔{3/2}×{√6/3}〕=
1+(1/2)×√6<1+(1/2)×√6.25
以下、Y切片が0になるケースとは、
1+(1/2)×√6.25
=1+(1/2)×2.5=1+1.25=2.25=4.5/2
であり、傾き「1+1/2×√6」のときY切片は正
になるから、合法であると、√6が√6.25になる
場合と比較して言える。
良く見ると判るが、(1,4)と(3,5)駒の傾
きTan(α)が1/2だと、有理化のときに、上記
のような事が起こるようである。
よって、いつもY切片の符号が、解き易くなるよう
には私には見えないが。
今回示したこの「式の整理」の存在により、方位角
比較法に比べて、三角関数正接の加法定理を使って、
2円の共通内接線の傾きを求めY切片の符号を計算す
る方法が、
暗算が極端に困難とまでは、言えない
ようになったと考える。
大学受験数学が得意な、将棋棋士と対局したときには、
相手が以上の式展開をした上で、厳密計算で合法手を
指したと主張したときには、相手の言い分を入れ、
諦めるしかこの新作将棋:奔将棋では、どうにも仕方
が無さそうだ。
現実には「2円の共通内接線のY切片が厳密に解け
る場合は、近似的方法で方位角を比較する方法に、着
手の合否は優先する」といった、ぼやかしたルールに
するしか、どうやら仕方無いように私には思えて来た。
(2023/11/08)
の暗算で頓挫」と、以前に述べた件の続きである。
普通に有理化すると、
1+√6/2<1+√6.25/2=2.25で、
4.5-2×2.25=0よりは大きいので、
y切片はプラスで、合法手になるようだ。
とんでもない大ボケを記事にしてしまったものだ。
一応詳しく書くと、以下のようになる。
{1/2+√(2/3)}/{1-1/2×√(2/3)}=
1/2{1+2√(2/3)}/{1-1/2×√(2/3)}=
ここから、普通に有理化すると、
1/2{1+2√(2/3)}{1+1/2×√(2/3)}/
〔{1-1/2×√(2/3)}{1+1/2×√(2/3)}〕=
1/2{1+2√(2/3)}{1+1/2×√(2/3)}/
〔1-1/4×(2/3)〕=
1/2{1+2√(2/3)}{1+1/2×√(2/3)}/
〔5/6〕=
3/5{1+2√(2/3)}{1+1/2×√(2/3)}=
3/5〔1+{2√(2/3)}+{1/2×√(2/3)}+{2/3}〕=
3/5〔1+{5/2×√(2/3)}+{2/3}〕=
3/5〔5/3+{5/2×√(2/3)}〕=
1+3/2×√(2/3)=1+〔{3/2}×{√6/3}〕=
1+(1/2)×√6<1+(1/2)×√6.25
以下、Y切片が0になるケースとは、
1+(1/2)×√6.25
=1+(1/2)×2.5=1+1.25=2.25=4.5/2
であり、傾き「1+1/2×√6」のときY切片は正
になるから、合法であると、√6が√6.25になる
場合と比較して言える。
良く見ると判るが、(1,4)と(3,5)駒の傾
きTan(α)が1/2だと、有理化のときに、上記
のような事が起こるようである。
よって、いつもY切片の符号が、解き易くなるよう
には私には見えないが。
今回示したこの「式の整理」の存在により、方位角
比較法に比べて、三角関数正接の加法定理を使って、
2円の共通内接線の傾きを求めY切片の符号を計算す
る方法が、
暗算が極端に困難とまでは、言えない
ようになったと考える。
大学受験数学が得意な、将棋棋士と対局したときには、
相手が以上の式展開をした上で、厳密計算で合法手を
指したと主張したときには、相手の言い分を入れ、
諦めるしかこの新作将棋:奔将棋では、どうにも仕方
が無さそうだ。
現実には「2円の共通内接線のY切片が厳密に解け
る場合は、近似的方法で方位角を比較する方法に、着
手の合否は優先する」といった、ぼやかしたルールに
するしか、どうやら仕方無いように私には思えて来た。
(2023/11/08)
2円の共通内接線を、幾何学で解いてみる(長さん)
今回は、数学の代数で2次方程式の根の公式で
答えを出した問題を、三角関数正接(Tan)
の加法定理を使い、かつ、代数ではなく幾何学
的に、図をイメージして解き、暗算が出来ない
かどうかを、チェックしたという話題である。
問題は既に本ブログで話題にした、半径が
1/√2で等しい2円の共通内接線の、傾きや、
y切片を求め、前記2円は排除円だとして、2
つの駒の隙間から、第3の取りたい相手の駒を、
どんな方向にも走れる超奔王という、仮想の駒
で取る手が、合法か、非合法かという判別を
目的としてものである。
意外だったが、tan(α+β)=
tan(α)+tan(β)/1-tan(α)×tan(β)
の、分子分母の割り算の暗算で、頓挫してしま
うという事が判った。
最後のあと一歩の所までは、
方位角の比較暗算よりも、図形がイメージ出来
れば、むしろ暗算の演算は早い
ようである。代数的に2円の内接線の方程式
を立てて、2次方程式の根の公式に代入する、
抽象的解き方よりは、かなり人間に、把握し
易くなる。
例として、(1,4)と(3,5)の駒で、
(3,7)の駒が隠れるかという問題で以下
に、今回テストしたやり方を説明する。
自駒金将前の歩兵駒を、取り捨ての位置まで
上げ、相手の桂馬前の歩兵と、上げた取り捨
て直前味方歩兵の2駒で、相手陣で初期位置
に居る桂馬位置の駒が、味方の超奔王で直射
するかどうかという例で示される問題である。
以前PCで(1,4)と(3,5)方位角
の比較をした結果から、略算で非合法になる
のに、厳密に角度を計算すると合法で、桂馬
位置の駒は見えているという事を示した、同
様な、精密/略算反転の例のうちの、一つで
ある。
このケース、人間には頭の中で、本来下記
のように回転させて、2円の中心を結ぶ線が、
水平になり、円中心同士の距離が√5である
という幾何学図は、公式から代数方程式を作
らなくても本来は、描けるはずである。
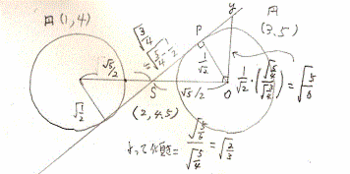
すると、図に書き込んだようなプロセスで、
円と円を結んだ線に対し、問題にしている2
円の共通内接線のうちの1本の傾きは、+
√2/3であると出せる。
ポイントは、垂線と円の中心のなす角と、
座標軸のxy軸のなす角は、共に垂直なので、
⊿OpSと⊿yOSとは相似であり、
Oy=Op×OS/Sp
のはずだという事である。そして
Sp=√(OSの2乗-Opの2乗)
である。傾きはSp/OSである。
そもそもy切片は、
2円の中点の座標(2,4.5)から、
4.5-傾き×2で簡単に出せる
ので、傾きが2.25以下ならy切片が
プラスになり、穴が見えてくる事までは、
幾何学イメージが出来ていれば頭の中で簡単
に思い浮かべる事が出来る。
ところが、その傾きだが、このケースには、
三角関数の正接の加法定理の公式:
tan(α+β)=
tan(α)+tan(β)/1-tan(α)×tan(β)
に代入し、求めようとすると、ちなみに
√(2/3)=2.44949/3=0.816・・
は、√6が「似よ良く良く」で暗算で出せ、
1/2+√(2/3)/1-(1/2×√2/3)
≒1.316・・/(1-0.408)
=1.316・・/0.592
となるのだが。
この1.316/0.592が2.25
より大きいのかどうか電卓が有れば2.22
前後で小さいと、一瞬で出るのだが、
暗算では、かなり面倒だと、私は疑う
のである。
以上1例だけだが。他でも正接(Tan)
の加法定理公式に代入時の割り算が、現実に
は暗算で、ネックになるのではないかと、私
は疑う。
本当に惜しいところだが、以上の点で同じ
半径円の共通内接線のy切片の計算よりも、
以前に示した方位角同士の比較計算の方が、
やはり、少しだけ勝っている
ように、私には依然として結論された。
代数計算は、円座標が実数で大きさがまちま
ちのときに、威力を発揮するが、同大きさ円
で中心座標が整数の如くに規則正しい時には、
幾何学図形を書いた方が、求め易いような気
がしたので、以上追加で、今回報告した次第
である。(2023/11/07)
答えを出した問題を、三角関数正接(Tan)
の加法定理を使い、かつ、代数ではなく幾何学
的に、図をイメージして解き、暗算が出来ない
かどうかを、チェックしたという話題である。
問題は既に本ブログで話題にした、半径が
1/√2で等しい2円の共通内接線の、傾きや、
y切片を求め、前記2円は排除円だとして、2
つの駒の隙間から、第3の取りたい相手の駒を、
どんな方向にも走れる超奔王という、仮想の駒
で取る手が、合法か、非合法かという判別を
目的としてものである。
意外だったが、tan(α+β)=
tan(α)+tan(β)/1-tan(α)×tan(β)
の、分子分母の割り算の暗算で、頓挫してしま
うという事が判った。
最後のあと一歩の所までは、
方位角の比較暗算よりも、図形がイメージ出来
れば、むしろ暗算の演算は早い
ようである。代数的に2円の内接線の方程式
を立てて、2次方程式の根の公式に代入する、
抽象的解き方よりは、かなり人間に、把握し
易くなる。
例として、(1,4)と(3,5)の駒で、
(3,7)の駒が隠れるかという問題で以下
に、今回テストしたやり方を説明する。
自駒金将前の歩兵駒を、取り捨ての位置まで
上げ、相手の桂馬前の歩兵と、上げた取り捨
て直前味方歩兵の2駒で、相手陣で初期位置
に居る桂馬位置の駒が、味方の超奔王で直射
するかどうかという例で示される問題である。
以前PCで(1,4)と(3,5)方位角
の比較をした結果から、略算で非合法になる
のに、厳密に角度を計算すると合法で、桂馬
位置の駒は見えているという事を示した、同
様な、精密/略算反転の例のうちの、一つで
ある。
このケース、人間には頭の中で、本来下記
のように回転させて、2円の中心を結ぶ線が、
水平になり、円中心同士の距離が√5である
という幾何学図は、公式から代数方程式を作
らなくても本来は、描けるはずである。

すると、図に書き込んだようなプロセスで、
円と円を結んだ線に対し、問題にしている2
円の共通内接線のうちの1本の傾きは、+
√2/3であると出せる。
ポイントは、垂線と円の中心のなす角と、
座標軸のxy軸のなす角は、共に垂直なので、
⊿OpSと⊿yOSとは相似であり、
Oy=Op×OS/Sp
のはずだという事である。そして
Sp=√(OSの2乗-Opの2乗)
である。傾きはSp/OSである。
そもそもy切片は、
2円の中点の座標(2,4.5)から、
4.5-傾き×2で簡単に出せる
ので、傾きが2.25以下ならy切片が
プラスになり、穴が見えてくる事までは、
幾何学イメージが出来ていれば頭の中で簡単
に思い浮かべる事が出来る。
ところが、その傾きだが、このケースには、
三角関数の正接の加法定理の公式:
tan(α+β)=
tan(α)+tan(β)/1-tan(α)×tan(β)
に代入し、求めようとすると、ちなみに
√(2/3)=2.44949/3=0.816・・
は、√6が「似よ良く良く」で暗算で出せ、
1/2+√(2/3)/1-(1/2×√2/3)
≒1.316・・/(1-0.408)
=1.316・・/0.592
となるのだが。
この1.316/0.592が2.25
より大きいのかどうか電卓が有れば2.22
前後で小さいと、一瞬で出るのだが、
暗算では、かなり面倒だと、私は疑う
のである。
以上1例だけだが。他でも正接(Tan)
の加法定理公式に代入時の割り算が、現実に
は暗算で、ネックになるのではないかと、私
は疑う。
本当に惜しいところだが、以上の点で同じ
半径円の共通内接線のy切片の計算よりも、
以前に示した方位角同士の比較計算の方が、
やはり、少しだけ勝っている
ように、私には依然として結論された。
代数計算は、円座標が実数で大きさがまちま
ちのときに、威力を発揮するが、同大きさ円
で中心座標が整数の如くに規則正しい時には、
幾何学図形を書いた方が、求め易いような気
がしたので、以上追加で、今回報告した次第
である。(2023/11/07)
青森県八戸市新むつ旅館に明治末将棋駒部屋札(長さん)
今回は、現在も使われている青森県八戸市
の太平洋戦争以前に遊郭であった現在の旅館
に、将棋と娼妓を引っ掛けたとされる、将棋
駒型の部屋番号札が、現在も使用されている
との旨の、以下の成書冒頭写真の紹介である。
鎌倉駅の現在駐輪場付近から、大将棋の定跡
を書いた飾り扇子が、風俗営業店を連想する
遺物と共出土するのも、将棋と娼妓の語音が
近いのと、関連が有る可能性もある。
成書の表題は以下の通りである。
「遊郭に泊まる」とんぼの本、㈱新潮社、
関根虎洸、西暦2018年。
写真は、上の成書の第9ページ付近に在り、
西暦2016年前後に撮影されたようである。
20箇所ほど旅館等で残っている施設が
紹介されているが、写真は第1番目の八戸
市の「新むつ旅館」の7号室を示す現存する
部屋番号札だとみられる。

なお青森県八戸市小中野6-20-18に
旅館は在るとの事である。
本ブログでは、鎌倉市鎌倉駅前駐輪所から
出土した遺物に、大将棋の指し方の定跡:「
斜め走駒で、仲人を突きぬいて右横行と反車
を排除し、相手陣から見て右端攻め耳破りで、
相手香車と飛車を更に剥がして、端の守りを
無力化してから、麒麟を上げて獅子に成らし
て、相手小駒を喰荒らして勝負をつける」の、
前半部分を書いた、本ブログ推定飾り扇子の
骨1本があり、付近が鎌倉時代に風俗営業店
の敷地内であったろうと推定している。
将棋は中国の唐代から賭博に使われていた
ので、風俗営業店で記念品の置き物に使う飾
り扇子に、大将棋の指し方のコツを墨書した
物品が有っても不思議は無いとの説明をした。
が、時代はぐっと下がって、前記成書の第
17ページ付近の記載により、今回紹介した
将棋駒に部屋番号を記載した物品は、明治末
の建築物の備品のようである。が、
将棋と娼妓がカケられたというのも、将棋と
風俗営業施設が関連する理由
の疑いを、持たせる史料という事にはなるよ
うだ。鎌倉時代にも、「娼妓」という熟語自
体は、存在皆無では無いだろうが。120年
と720年とでは6倍も違うので、残念なが
ら、決定打では無い。それが理由で元の風俗
営業店からは将棋関連史料が出土する例が有
りえるという、可能性を示したに留まるだろ
うと、思われるという事である。(2023/11/06)
の太平洋戦争以前に遊郭であった現在の旅館
に、将棋と娼妓を引っ掛けたとされる、将棋
駒型の部屋番号札が、現在も使用されている
との旨の、以下の成書冒頭写真の紹介である。
鎌倉駅の現在駐輪場付近から、大将棋の定跡
を書いた飾り扇子が、風俗営業店を連想する
遺物と共出土するのも、将棋と娼妓の語音が
近いのと、関連が有る可能性もある。
成書の表題は以下の通りである。
「遊郭に泊まる」とんぼの本、㈱新潮社、
関根虎洸、西暦2018年。
写真は、上の成書の第9ページ付近に在り、
西暦2016年前後に撮影されたようである。
20箇所ほど旅館等で残っている施設が
紹介されているが、写真は第1番目の八戸
市の「新むつ旅館」の7号室を示す現存する
部屋番号札だとみられる。

なお青森県八戸市小中野6-20-18に
旅館は在るとの事である。
本ブログでは、鎌倉市鎌倉駅前駐輪所から
出土した遺物に、大将棋の指し方の定跡:「
斜め走駒で、仲人を突きぬいて右横行と反車
を排除し、相手陣から見て右端攻め耳破りで、
相手香車と飛車を更に剥がして、端の守りを
無力化してから、麒麟を上げて獅子に成らし
て、相手小駒を喰荒らして勝負をつける」の、
前半部分を書いた、本ブログ推定飾り扇子の
骨1本があり、付近が鎌倉時代に風俗営業店
の敷地内であったろうと推定している。
将棋は中国の唐代から賭博に使われていた
ので、風俗営業店で記念品の置き物に使う飾
り扇子に、大将棋の指し方のコツを墨書した
物品が有っても不思議は無いとの説明をした。
が、時代はぐっと下がって、前記成書の第
17ページ付近の記載により、今回紹介した
将棋駒に部屋番号を記載した物品は、明治末
の建築物の備品のようである。が、
将棋と娼妓がカケられたというのも、将棋と
風俗営業施設が関連する理由
の疑いを、持たせる史料という事にはなるよ
うだ。鎌倉時代にも、「娼妓」という熟語自
体は、存在皆無では無いだろうが。120年
と720年とでは6倍も違うので、残念なが
ら、決定打では無い。それが理由で元の風俗
営業店からは将棋関連史料が出土する例が有
りえるという、可能性を示したに留まるだろ
うと、思われるという事である。(2023/11/06)
一定半径で格子状に整数座標配置円の内接線暗算の難易(長さん)
これまで、一定半径で格子状に整数座標で
配置された2円の共通外接線は、Y切片の
数値・符号の暗算が公式の存在により容易
であり、向こう側の円の手前円による遮蔽
を調べるのに、各円の接線方位角を比較す
るよりも、原点を遮蔽状態の観測点とし、
公式で、共通外接線のY切片を求めて、
円同士の、見え隠れを推定した方が、簡単
である事を示した。
観測点(超奔王駒位置)を(0,0)と
し、近傍円、遠方円の位置をそれぞれ
(m1,n1)(m2,n2)としたとき、
排除円が半径√2なら、直線の傾きAは、
共通外接線について、
A=n2-n1/(m2-m1)
と、円の半径が常に√2の為簡単になり、
Y切片Bは、
B=n1-A×m1干√Aの2乗+1/√2
と、比較の為方位角を求めるよりも、ごく
簡単だったという事だった。
では、外接線ではなく、内接線で、第3
の駒が超奔王にとってターゲットであり、
2つの駒の「穴」から、第3ターゲット駒
が覗いているのかという問題で、遮蔽駒の
「穴」の有無を調べるための、今度は、
2円共通内接線は、以前に本ブログで簡単
にコメントしたように、暗算困難というの
は、本当なのかを、今回は以下のように、
詳しくチェックしてみた。
2円共通内接線を計算せずに
方位角同士の比較暗算した方が、やはり楽
なようである。
今回も、以前に引き続いて、以下の受験
数学のwebサイトをチェック/トレース
するという方法で、上記点を確かめた。
「大学受験数学自学自習応援: 難関大入試問題
と解答2019:2円の共通接線愛知教育大」
エイチティティピーエス://suugakujigaku.com/
外接線の場合は、2点は式を求める直線
の同じ側に有るのだが、内接線では円の中
心である2点が、反対側に有るので、それ
ぞれ2点から√2距離になる直線の方程式
を求めようとして、連立方程式を立て、左
辺を等しいと置いても、それらの絶対値が
等しくても、距離の符号が逆の場合となり、
共通外接線の場合と異なり、共通内接線で
はY切片の未知数bが消去出来ずに、2倍
のまま残る。
そこで、移項したあと1/2して、連立
方程式の一方に辺々を足すという、普通だ
が、そのやり方でBを消去するが。
左辺の分母を掛けると、√の中にAの2乗
が入る形となる為、左右式を2乗して、直
線の式の傾きAは2次方程式にして、根の
公式から求めなければならず、
ax^2+bx+c=0のa,b,cは、
それぞれ、以下のようにかなり複雑化する。
aは1/4{(m2-m1)(m2-m1)-2}
のような形。{}内は、20~30の整数。
bは、-1/2×(m2-m1)(n2-n1)
のような形。()の2乗でやはり、何十で
あるが、多分負の数である。
cは、1/4{(n2-n1)(n2-n1)-2}
になり、{}内は、20~30の整数。
「=0」なので、1/4倍は消去可能と考
えられる。
また、ここでbが偶数になるので、
x=-(b/2)±√{(b/2)(b/2)-ac}/a
という根の公式の変形式が、たぶん使える
パターンだとみられる。
そこで、問題は
-(b/2)/a±√(b/2)(b/2)-ac/a
としたときの、
√{(b/2)(b/2)-ac}/aの暗
算だとみられるが、暗算し易くするため、
√〔{(b/2)(b/2)-ac}/(a×a)〕
としたとして、分母も分子も、一千何百と
いう数の程度だと私は思う。この暗算は、
1か2の一桁の整数が答えになるのだろう
が、割る数の桁が多いため、以前述べた
方位角の暗算に比べて、かなりしんどい
はずである。計算自体が、対局を多数繰り
返すと、何回も同じ計算をする事になる
のは、方位角計算も、接線の傾き・Y切片
計算も同じだとは思えるのだが。
そして後で、-(b/2)/aを足す
わけだが、中心点の方位角を足す手間の
程度だろう。
なお、これで出るのはY切片では無く
て、傾きAであるから、たぶん
B=(n1+n2)-A(m1+m2)/2
だと見られる公式で、更に計算すると、
Y切片が、ようやく求められるようだ。
何れにしても、2円の共通内接線の直線
の、傾きを求める為の、二次方程式の、
平方根の中身の割算暗算が、方位角比較
方法よりも、相当困難になるのが致命的
なように、私には見える。
よって2つの駒で、第3の駒が見えて、
超奔王を2駒を突き抜けさせて、駒が取
れるかどうかというルールについては、
以前述べた、方位角の比較方法を取る事
にした方が、やはり良いように思えた。
確か3例、厳密に計算したときに対し
て、本当は「合法手」が「非合法手」と
真逆の結論になって矛盾してしまうが。
近似計算結果の「非合法」の方をルール
とみなして、それらのケースは我慢せざる
を、得ないのではないだろうかと、私は
考える。(2023/11/05)
配置された2円の共通外接線は、Y切片の
数値・符号の暗算が公式の存在により容易
であり、向こう側の円の手前円による遮蔽
を調べるのに、各円の接線方位角を比較す
るよりも、原点を遮蔽状態の観測点とし、
公式で、共通外接線のY切片を求めて、
円同士の、見え隠れを推定した方が、簡単
である事を示した。
観測点(超奔王駒位置)を(0,0)と
し、近傍円、遠方円の位置をそれぞれ
(m1,n1)(m2,n2)としたとき、
排除円が半径√2なら、直線の傾きAは、
共通外接線について、
A=n2-n1/(m2-m1)
と、円の半径が常に√2の為簡単になり、
Y切片Bは、
B=n1-A×m1干√Aの2乗+1/√2
と、比較の為方位角を求めるよりも、ごく
簡単だったという事だった。
では、外接線ではなく、内接線で、第3
の駒が超奔王にとってターゲットであり、
2つの駒の「穴」から、第3ターゲット駒
が覗いているのかという問題で、遮蔽駒の
「穴」の有無を調べるための、今度は、
2円共通内接線は、以前に本ブログで簡単
にコメントしたように、暗算困難というの
は、本当なのかを、今回は以下のように、
詳しくチェックしてみた。
2円共通内接線を計算せずに
方位角同士の比較暗算した方が、やはり楽
なようである。
今回も、以前に引き続いて、以下の受験
数学のwebサイトをチェック/トレース
するという方法で、上記点を確かめた。
「大学受験数学自学自習応援: 難関大入試問題
と解答2019:2円の共通接線愛知教育大」
エイチティティピーエス://suugakujigaku.com/
外接線の場合は、2点は式を求める直線
の同じ側に有るのだが、内接線では円の中
心である2点が、反対側に有るので、それ
ぞれ2点から√2距離になる直線の方程式
を求めようとして、連立方程式を立て、左
辺を等しいと置いても、それらの絶対値が
等しくても、距離の符号が逆の場合となり、
共通外接線の場合と異なり、共通内接線で
はY切片の未知数bが消去出来ずに、2倍
のまま残る。
そこで、移項したあと1/2して、連立
方程式の一方に辺々を足すという、普通だ
が、そのやり方でBを消去するが。
左辺の分母を掛けると、√の中にAの2乗
が入る形となる為、左右式を2乗して、直
線の式の傾きAは2次方程式にして、根の
公式から求めなければならず、
ax^2+bx+c=0のa,b,cは、
それぞれ、以下のようにかなり複雑化する。
aは1/4{(m2-m1)(m2-m1)-2}
のような形。{}内は、20~30の整数。
bは、-1/2×(m2-m1)(n2-n1)
のような形。()の2乗でやはり、何十で
あるが、多分負の数である。
cは、1/4{(n2-n1)(n2-n1)-2}
になり、{}内は、20~30の整数。
「=0」なので、1/4倍は消去可能と考
えられる。
また、ここでbが偶数になるので、
x=-(b/2)±√{(b/2)(b/2)-ac}/a
という根の公式の変形式が、たぶん使える
パターンだとみられる。
そこで、問題は
-(b/2)/a±√(b/2)(b/2)-ac/a
としたときの、
√{(b/2)(b/2)-ac}/aの暗
算だとみられるが、暗算し易くするため、
√〔{(b/2)(b/2)-ac}/(a×a)〕
としたとして、分母も分子も、一千何百と
いう数の程度だと私は思う。この暗算は、
1か2の一桁の整数が答えになるのだろう
が、割る数の桁が多いため、以前述べた
方位角の暗算に比べて、かなりしんどい
はずである。計算自体が、対局を多数繰り
返すと、何回も同じ計算をする事になる
のは、方位角計算も、接線の傾き・Y切片
計算も同じだとは思えるのだが。
そして後で、-(b/2)/aを足す
わけだが、中心点の方位角を足す手間の
程度だろう。
なお、これで出るのはY切片では無く
て、傾きAであるから、たぶん
B=(n1+n2)-A(m1+m2)/2
だと見られる公式で、更に計算すると、
Y切片が、ようやく求められるようだ。
何れにしても、2円の共通内接線の直線
の、傾きを求める為の、二次方程式の、
平方根の中身の割算暗算が、方位角比較
方法よりも、相当困難になるのが致命的
なように、私には見える。
よって2つの駒で、第3の駒が見えて、
超奔王を2駒を突き抜けさせて、駒が取
れるかどうかというルールについては、
以前述べた、方位角の比較方法を取る事
にした方が、やはり良いように思えた。
確か3例、厳密に計算したときに対し
て、本当は「合法手」が「非合法手」と
真逆の結論になって矛盾してしまうが。
近似計算結果の「非合法」の方をルール
とみなして、それらのケースは我慢せざる
を、得ないのではないだろうかと、私は
考える。(2023/11/05)
円共通外接線のY切片は円半径等しいと計算簡単(長さん)
これまで本ブログでは、あらゆる方向に走れる
超奔王の進路を塞ぐ「間駒・途中駒」の計算に、
方位角度の比較を行う方法を提案してきた。
しかし、近似的にしか答えの出ない方法では
無く、ターゲット駒の見え隠れと、途中駒の見
え隠れは、
共通接線のY切片を求める公式が、排除円半径
が、常に一定(1/√2)である場合は暗算し
易い形で存在する事が、web上の大学入試数
学サイトの調査で判った
ので、以下に紹介する。
排除円半径遠方42°逆比例近似計算は、2つ
の駒の見え隠れを計算するケースには、使用する
必要が無い
ようだ。
公式は、
B=n1-A×m1干√(Aの2乗+1)/√2
となるようだ。
円共通接線の大学入試問題を読んで、参考にし
たwebサイトは、次の通りである。
「大学受験数学自学自習応援: 難関大入試問題
と解答2019:2円の共通接線愛知教育大」
エイチティティピーエス://suugakujigaku.com/
ようするに、視線に対応する、本ブログで示
した「共通外接線」は、
上限部分も下限部分も、円の半径が等しいとき
には、外接線が単純に円同士を結んだ線と、傾
きAが同じ
なのであった。
その為、外接線のY切片Bは、円の中心座標
をそれぞれ(m1,n1)、(m2,n2)と
して、傾きから外接線の場合には、
A=(n2-n1)/(m2-m1)
で求めてしまうと、点からの直線の距離の式で、
連立させてBを解く場合に、外接線で符号が正
になるときには、単純にAが求まった後、Bが、
冒頭の式になってしまうだけなのである。内接
線で符号が負になるときには、未知数のBが、
残るので、解くのには2次方程式の根の公式が
必要になる。内接線のケース、つまり2つの将
棋駒の間を超奔王が、すり抜けられるかどうか
を計算する場合には、恐らく暗算するとすれば、
本ブログのやり方の方が、楽だろう。
以上は本ブログ管理人の、大きな見落とし
だった。だから、
外接線の動向を、超奔王の居る原点について考
える為、Y切片を計算すれば、方位角を比較し
無くても、
Y切片の符号から判断しさえすれば単純に駒1
個で、向こう側の駒が、超奔王から見て隠れる
かどうかを調べるときには、それで済む
のである。
例を、超奔王先の歩兵を2歩上げて、超奔王
位置から3の0駒で、相手金将、7の1駒が隠
れるかどうかという例で、以下示す。方位角を
求める近似計算では、隠れてしまう錯誤があっ
たのであった。
B=3-0-√4の2乗+1/√2でマイナス
になるのか、というこれだけの事である。
√4の2乗+1=√17≒4+1/8
=4.125であり、
B=3-0-4.125/√2
>3-0-4.125×0.71
≒3-2.9285=0.0715>0である
から、暗算で
3の0駒から7の1駒は、見えると簡単に出る。
この計算は、近似が基本的な部分で無い。
以上の点から、単純に向こうの駒が、手前の
1個の駒で重なった結果として隠れるかとうか
のケースについては、半径の等しい円の外接線
の、上記公式から判断し、
方位角の比較から判断した、本ブログのやり方
は、使わないのが道理
だと、訂正せざるを得ないという事になったと
私は考える。これまでの本ブログの記事には、
大きな回り道が有ったという事になる。(2023/11/04)
超奔王の進路を塞ぐ「間駒・途中駒」の計算に、
方位角度の比較を行う方法を提案してきた。
しかし、近似的にしか答えの出ない方法では
無く、ターゲット駒の見え隠れと、途中駒の見
え隠れは、
共通接線のY切片を求める公式が、排除円半径
が、常に一定(1/√2)である場合は暗算し
易い形で存在する事が、web上の大学入試数
学サイトの調査で判った
ので、以下に紹介する。
排除円半径遠方42°逆比例近似計算は、2つ
の駒の見え隠れを計算するケースには、使用する
必要が無い
ようだ。
公式は、
B=n1-A×m1干√(Aの2乗+1)/√2
となるようだ。
円共通接線の大学入試問題を読んで、参考にし
たwebサイトは、次の通りである。
「大学受験数学自学自習応援: 難関大入試問題
と解答2019:2円の共通接線愛知教育大」
エイチティティピーエス://suugakujigaku.com/
ようするに、視線に対応する、本ブログで示
した「共通外接線」は、
上限部分も下限部分も、円の半径が等しいとき
には、外接線が単純に円同士を結んだ線と、傾
きAが同じ
なのであった。
その為、外接線のY切片Bは、円の中心座標
をそれぞれ(m1,n1)、(m2,n2)と
して、傾きから外接線の場合には、
A=(n2-n1)/(m2-m1)
で求めてしまうと、点からの直線の距離の式で、
連立させてBを解く場合に、外接線で符号が正
になるときには、単純にAが求まった後、Bが、
冒頭の式になってしまうだけなのである。内接
線で符号が負になるときには、未知数のBが、
残るので、解くのには2次方程式の根の公式が
必要になる。内接線のケース、つまり2つの将
棋駒の間を超奔王が、すり抜けられるかどうか
を計算する場合には、恐らく暗算するとすれば、
本ブログのやり方の方が、楽だろう。
以上は本ブログ管理人の、大きな見落とし
だった。だから、
外接線の動向を、超奔王の居る原点について考
える為、Y切片を計算すれば、方位角を比較し
無くても、
Y切片の符号から判断しさえすれば単純に駒1
個で、向こう側の駒が、超奔王から見て隠れる
かどうかを調べるときには、それで済む
のである。
例を、超奔王先の歩兵を2歩上げて、超奔王
位置から3の0駒で、相手金将、7の1駒が隠
れるかどうかという例で、以下示す。方位角を
求める近似計算では、隠れてしまう錯誤があっ
たのであった。
B=3-0-√4の2乗+1/√2でマイナス
になるのか、というこれだけの事である。
√4の2乗+1=√17≒4+1/8
=4.125であり、
B=3-0-4.125/√2
>3-0-4.125×0.71
≒3-2.9285=0.0715>0である
から、暗算で
3の0駒から7の1駒は、見えると簡単に出る。
この計算は、近似が基本的な部分で無い。
以上の点から、単純に向こうの駒が、手前の
1個の駒で重なった結果として隠れるかとうか
のケースについては、半径の等しい円の外接線
の、上記公式から判断し、
方位角の比較から判断した、本ブログのやり方
は、使わないのが道理
だと、訂正せざるを得ないという事になったと
私は考える。これまでの本ブログの記事には、
大きな回り道が有ったという事になる。(2023/11/04)
奔将棋超奔王の「間駒」排除視半径42割算方法(長さん)
本ブログで考案した奔将棋では、ただ1種類だが
超奔王が、1升目離れたところで排除角42°に
見える半径√2/2升の間の駒/途中の駒の排除
円を、すり抜けられるかどうかで、ターゲット駒
を取るという着手の、合法/非合法が決まるとし
ている。
こんないっけん、めんどうなルールにしたのは、
産業革命をもたらしたワットの蒸気機関の物理学
の原理ともなっている、気体の分子運動論という
近代科学を、近世的な日本のいわゆる将棋に導入
することが、ゲームの近代化とか応用の広がり等
を考えると、少なくとも教育との関連で、明らか
に意義が大きく、その為やむをえないというのが、
本ブログの管理人の見方だからである。
その為、暗算で42の2乗を割るという作業が
頭の中で必要になり、除数113を例に引いたが、
将棋型のゲームを楽しむには、割り算の暗算が、
意外にネックになるという結論だった。
そこで今回は、
その小学校の割り算の暗算について、考えてみる。
ただし、以下は1764という特定の数が、
割られる数である場合にだけ、有用である。
なお1764は42の2乗であり、42×42
44×40+2×2=1760+4=1764
と暗算すると良いとの情報が、複数の成書に有る。
なお元々
42=2×3×7なので。
1764=2^2+3^2+7^2であり、
1764/2=882、1764/4=441、
1764/3=588、1764/9=196、
1764/7=252は、覚えておくとよさそう
である。また1764×2=3528である。
暗算は、割る数を2~3%に抑えて別の、素
因数分解し易い数に替え、約分して計算を簡単に
し、簡単になった割り算を暗算後誤差分を乗せて、
開平作業工程に移す。
7の8の視半径、√1764/113をこの
やり方で、やり直すと以下の通り。
113は112より1%弱大きい。112で代用。
112=7×16、1764/7=252、
252/4=63、63/4=15.75で1%
小さく1764/113=15.6。今度は、
あっという間に概算の割り算が出来た。
√15.6=4-0.4/8=3.95程度と、
むしろ開平計算の方は以前の述べたが簡単に出る。
以下、8の6・・・8の1とやってみる。
8の6は、ピタゴラスの三角形で距離10であ
るから4.2°。
8の5は、√1764/89。90で代用する
と、1764/90=19.6であり、1%強
割る数が小さいから19.8前後。
√19.8は、4.4×4.4=4.8×4+0.16
=19.36であり、4.4+0.44/8.8
=4.45。
8の4は2の1の4倍であり、2の1のときは、
18.782971であったから、4.7前後。
8の3は、√1764/73。72で代用。
1.4%程度大きく出るが、72=9×8であり、
1764/9=196、196/8=24.5。
そこで24.2程度。
√24.2=5-0.8/10=4.92位。
8の2は4の1の2倍。4の1は10.18で
あったから、5.09位。
8の1は、8の0が5.25で、1は64の
1/64で、ルートのとき寄与は1/128。
よって、5.20前後と見られる。以下辺に近い
ケースは、この方法も使用出来るとみられる。
8の0は、5.25°。
7の6以下は、次のようになる。
7の6は、√1764/85で、84で代用
する。84=42×2であるから、√21で、
1%強小さい、√20.8前後になるとみられる。
4.5×4.5=4×5+0.25=20.25
と暗算せよとの情報が複数あり、
√20.8=4.5+0.55/9=4.56
前後とみられる。
7の5は、√1764/74で、75で代用
すると、1764/3=588、588×4=
1176×2=2352であるから、
1764/75=23.52とみられ、
1764/74=23.8前後と見られる。
よって、√23.8=5-1.2/10
=4.88前後とみられる。
7の4は、√1764/63で63は7×9
であるから、1764/63=252/9=28
である。√28=2√7=2×2.64575
=5.29前後とみられる。(√7は、
「ルート菜、に虫いつ無い」)
7の3は、√1764/58で60で代用。
1/30前後大きいとみられる。1764/60
=588/20=29.4で、30.4位だと
みられる。5.5×5.5=30.25であり、
√30.4=5.5+0.15/11
=5.514前後と見られる。
7の2は、√1764/53で53を50で
代用すると、1764/50=35.28より
6%小さく、33.3前後とみられる。
よって√33.3=6-2.7/12
=5.775前後とみられる。
7の1は、7の0のとき6であり、1の寄与は、
1%(1/49/2)程度とみられ、5.94
前後とみられる。
7の0は、6である。
6の5は、√1764/61であり、60で
代用。前記7の3と同じであり、1764/6=
29.4で、1/60小さいはずで、28.9。
√28.9=5.5-1.35/11=5.38
前後。または、√28.9=5+3.9/10
=5.39で、後者でも良いが、5.5から持っ
ていった方が、誤差は少し少ないようである。
6の4は、3の2の2倍であり、3の2は、
11.64870(いい虫は慣れ)であったから、
その2分の1で、5.82程度とみられる。
6の3は、2の1の3倍であり、
18.782971の3分の1で、6.26程度
とみられる。
6の2は3の1の2倍であり、3の1は、
13.28であるから、6.64前後とみられる。
6の1はルート内の36に対する1の寄与は、
1/72程度であるから、7+7/72=6.9
前後であり、既にその旨本プログに書いている。
以下5の4からは記憶するとの事だった。つ
まり、5の4を6.66、5の3を7.28294、
5の2を7.8、5の1を8.24、5の0が
8.4と記憶。
4の3からは、4の3はピタゴラスで5。
4の2は2の1の2倍で、9.39。4の1は、
10.18と記憶、4の0は10.5。
3以下は、3の2が11.64870、
3の1が13.28、3の0が14。2の1が、
18.782971。2の0が21。1の1は、
ぴたりと30°、1の0が45°。以上しか、
9×9升目盤には、存在し無いのである。
上記書いている本ブログの管理人が、そのうち
内容を忘れるだろうが。これしか無いのだから、
やり直しているうちに、常に正しく計算できる
ようになる事は、明らかだと考える。(2023/11/03)
超奔王が、1升目離れたところで排除角42°に
見える半径√2/2升の間の駒/途中の駒の排除
円を、すり抜けられるかどうかで、ターゲット駒
を取るという着手の、合法/非合法が決まるとし
ている。
こんないっけん、めんどうなルールにしたのは、
産業革命をもたらしたワットの蒸気機関の物理学
の原理ともなっている、気体の分子運動論という
近代科学を、近世的な日本のいわゆる将棋に導入
することが、ゲームの近代化とか応用の広がり等
を考えると、少なくとも教育との関連で、明らか
に意義が大きく、その為やむをえないというのが、
本ブログの管理人の見方だからである。
その為、暗算で42の2乗を割るという作業が
頭の中で必要になり、除数113を例に引いたが、
将棋型のゲームを楽しむには、割り算の暗算が、
意外にネックになるという結論だった。
そこで今回は、
その小学校の割り算の暗算について、考えてみる。
ただし、以下は1764という特定の数が、
割られる数である場合にだけ、有用である。
なお1764は42の2乗であり、42×42
44×40+2×2=1760+4=1764
と暗算すると良いとの情報が、複数の成書に有る。
なお元々
42=2×3×7なので。
1764=2^2+3^2+7^2であり、
1764/2=882、1764/4=441、
1764/3=588、1764/9=196、
1764/7=252は、覚えておくとよさそう
である。また1764×2=3528である。
暗算は、割る数を2~3%に抑えて別の、素
因数分解し易い数に替え、約分して計算を簡単に
し、簡単になった割り算を暗算後誤差分を乗せて、
開平作業工程に移す。
7の8の視半径、√1764/113をこの
やり方で、やり直すと以下の通り。
113は112より1%弱大きい。112で代用。
112=7×16、1764/7=252、
252/4=63、63/4=15.75で1%
小さく1764/113=15.6。今度は、
あっという間に概算の割り算が出来た。
√15.6=4-0.4/8=3.95程度と、
むしろ開平計算の方は以前の述べたが簡単に出る。
以下、8の6・・・8の1とやってみる。
8の6は、ピタゴラスの三角形で距離10であ
るから4.2°。
8の5は、√1764/89。90で代用する
と、1764/90=19.6であり、1%強
割る数が小さいから19.8前後。
√19.8は、4.4×4.4=4.8×4+0.16
=19.36であり、4.4+0.44/8.8
=4.45。
8の4は2の1の4倍であり、2の1のときは、
18.782971であったから、4.7前後。
8の3は、√1764/73。72で代用。
1.4%程度大きく出るが、72=9×8であり、
1764/9=196、196/8=24.5。
そこで24.2程度。
√24.2=5-0.8/10=4.92位。
8の2は4の1の2倍。4の1は10.18で
あったから、5.09位。
8の1は、8の0が5.25で、1は64の
1/64で、ルートのとき寄与は1/128。
よって、5.20前後と見られる。以下辺に近い
ケースは、この方法も使用出来るとみられる。
8の0は、5.25°。
7の6以下は、次のようになる。
7の6は、√1764/85で、84で代用
する。84=42×2であるから、√21で、
1%強小さい、√20.8前後になるとみられる。
4.5×4.5=4×5+0.25=20.25
と暗算せよとの情報が複数あり、
√20.8=4.5+0.55/9=4.56
前後とみられる。
7の5は、√1764/74で、75で代用
すると、1764/3=588、588×4=
1176×2=2352であるから、
1764/75=23.52とみられ、
1764/74=23.8前後と見られる。
よって、√23.8=5-1.2/10
=4.88前後とみられる。
7の4は、√1764/63で63は7×9
であるから、1764/63=252/9=28
である。√28=2√7=2×2.64575
=5.29前後とみられる。(√7は、
「ルート菜、に虫いつ無い」)
7の3は、√1764/58で60で代用。
1/30前後大きいとみられる。1764/60
=588/20=29.4で、30.4位だと
みられる。5.5×5.5=30.25であり、
√30.4=5.5+0.15/11
=5.514前後と見られる。
7の2は、√1764/53で53を50で
代用すると、1764/50=35.28より
6%小さく、33.3前後とみられる。
よって√33.3=6-2.7/12
=5.775前後とみられる。
7の1は、7の0のとき6であり、1の寄与は、
1%(1/49/2)程度とみられ、5.94
前後とみられる。
7の0は、6である。
6の5は、√1764/61であり、60で
代用。前記7の3と同じであり、1764/6=
29.4で、1/60小さいはずで、28.9。
√28.9=5.5-1.35/11=5.38
前後。または、√28.9=5+3.9/10
=5.39で、後者でも良いが、5.5から持っ
ていった方が、誤差は少し少ないようである。
6の4は、3の2の2倍であり、3の2は、
11.64870(いい虫は慣れ)であったから、
その2分の1で、5.82程度とみられる。
6の3は、2の1の3倍であり、
18.782971の3分の1で、6.26程度
とみられる。
6の2は3の1の2倍であり、3の1は、
13.28であるから、6.64前後とみられる。
6の1はルート内の36に対する1の寄与は、
1/72程度であるから、7+7/72=6.9
前後であり、既にその旨本プログに書いている。
以下5の4からは記憶するとの事だった。つ
まり、5の4を6.66、5の3を7.28294、
5の2を7.8、5の1を8.24、5の0が
8.4と記憶。
4の3からは、4の3はピタゴラスで5。
4の2は2の1の2倍で、9.39。4の1は、
10.18と記憶、4の0は10.5。
3以下は、3の2が11.64870、
3の1が13.28、3の0が14。2の1が、
18.782971。2の0が21。1の1は、
ぴたりと30°、1の0が45°。以上しか、
9×9升目盤には、存在し無いのである。
上記書いている本ブログの管理人が、そのうち
内容を忘れるだろうが。これしか無いのだから、
やり直しているうちに、常に正しく計算できる
ようになる事は、明らかだと考える。(2023/11/03)
本ブログの表題「縁台将棋普及団体」ページと衝突(長さん)
以前に以下の点説明したが、本ブログの表題の
意味する「大将棋」の読みは、だいしょうぎで
も、おおしょうぎでも、正しいというのが、
本ブログの主張である。現代の、大型国語辞書
の調査を根拠としている。
ただし本ブログの題字が「だい将棋」に
なっているのも、それなりの根拠が在るとして
いる。 高段者の将棋のタイトルの掛かった、
大一番等で、接戦で勝者が決まる場合に、
「大将棋」と書いて、「おおしょうぎ」と読む
と管理人が認識しているからである。プロ将棋
の観戦記で、たまに見かける言い回しだと認識
している。本ブログとキ-ワードとして衝突す
るので禁止表現にするというのも無理だろうし、
その程度の理由で止めろと言っては、言論の
弾圧の類であり、無理だと考えて本ブログが引
いたという事である。
その他に、Google検索したとき、各
大学将棋部のサイトの題字のワードと、衝突し
にくいというメリットが「だい将棋」には有る。
小生の家から「大将棋」を検索すると、現時
点で「京都大学将棋部のトップページ」が、私
のこのブログよりも、Google検索で上位
に来る。20年近く前のweb出来立ての大学
サイト中心の時代には、完全に大学将棋部のサ
イトに、数や順位で圧倒されていた。
そこで本ブログの題字は「だい将棋」にして、
正直安閑としていたのだが。最近「縁台将棋の
普及団体」のトップページ等が、時代の流れで、
縁台では意味不明となったのか、「縁台将棋」
では無く「えんだい将棋」と、表現するように
なったらしい。その為、普段から自分のブログ
に頻繁にアクセスする、本ブログ管理人の家か
らは別として、恐らくよそからGoogle検
索すると、「えんだい将棋」が「だい将棋」と
衝突して、このブログは下位に転落している模
様である。
そこでその対策だが、少し考えた末
しばらく放置して様子を見る事にした。
公園等で、今でも類似の機能を持つ物品:
「背モタレの無いベンチ」を、個人的に見かけ
るので。少なくとも
漢字の「縁台」が日本で消滅語になったとすれ
ば、それ自身は興味深い社会現象
のような気が、私にはするのである。
恐らく縁側とか濡れ縁とかいう言い方を、余
りし無くなったから、それに付随して衰微しつ
つあるのかもしれないが。間取りによって建売
住宅などでも、今も縁台はこの漢字の表現で使
う場合がありかつ、対応外来語も「移動」の性
格の無いウッドデッキと違うから、取り立てて
現状無いと、個人的には考えている。なので、
縁台という単語自体は
消滅しそうになったら、ナゼだ
と皆が気がつくのではないかという事である。
そして、少なくとも
漢字自体も単純なものではないのかと私は疑う。
そこで、他にひらがなにした理由も考えにく
いので。無くなるのを読んで、親しみやすく
すればよいかとひらがなに変えているように私
には見えるが。その行為は、杞憂なのかもしれ
ないと、私は疑っているのである。
以上を精密に議論をするとすればきりが無い
し、それほどのものでも無いと私は考えるので。
しばらく放置すれば、そのうち「縁台将棋」に
変わるのではないかと、密かに疑っていれば、
時が解決するのでそれで良い
と考えた。以上のような思考を、私はしたとい
う事である。(2023/11/02)
意味する「大将棋」の読みは、だいしょうぎで
も、おおしょうぎでも、正しいというのが、
本ブログの主張である。現代の、大型国語辞書
の調査を根拠としている。
ただし本ブログの題字が「だい将棋」に
なっているのも、それなりの根拠が在るとして
いる。 高段者の将棋のタイトルの掛かった、
大一番等で、接戦で勝者が決まる場合に、
「大将棋」と書いて、「おおしょうぎ」と読む
と管理人が認識しているからである。プロ将棋
の観戦記で、たまに見かける言い回しだと認識
している。本ブログとキ-ワードとして衝突す
るので禁止表現にするというのも無理だろうし、
その程度の理由で止めろと言っては、言論の
弾圧の類であり、無理だと考えて本ブログが引
いたという事である。
その他に、Google検索したとき、各
大学将棋部のサイトの題字のワードと、衝突し
にくいというメリットが「だい将棋」には有る。
小生の家から「大将棋」を検索すると、現時
点で「京都大学将棋部のトップページ」が、私
のこのブログよりも、Google検索で上位
に来る。20年近く前のweb出来立ての大学
サイト中心の時代には、完全に大学将棋部のサ
イトに、数や順位で圧倒されていた。
そこで本ブログの題字は「だい将棋」にして、
正直安閑としていたのだが。最近「縁台将棋の
普及団体」のトップページ等が、時代の流れで、
縁台では意味不明となったのか、「縁台将棋」
では無く「えんだい将棋」と、表現するように
なったらしい。その為、普段から自分のブログ
に頻繁にアクセスする、本ブログ管理人の家か
らは別として、恐らくよそからGoogle検
索すると、「えんだい将棋」が「だい将棋」と
衝突して、このブログは下位に転落している模
様である。
そこでその対策だが、少し考えた末
しばらく放置して様子を見る事にした。
公園等で、今でも類似の機能を持つ物品:
「背モタレの無いベンチ」を、個人的に見かけ
るので。少なくとも
漢字の「縁台」が日本で消滅語になったとすれ
ば、それ自身は興味深い社会現象
のような気が、私にはするのである。
恐らく縁側とか濡れ縁とかいう言い方を、余
りし無くなったから、それに付随して衰微しつ
つあるのかもしれないが。間取りによって建売
住宅などでも、今も縁台はこの漢字の表現で使
う場合がありかつ、対応外来語も「移動」の性
格の無いウッドデッキと違うから、取り立てて
現状無いと、個人的には考えている。なので、
縁台という単語自体は
消滅しそうになったら、ナゼだ
と皆が気がつくのではないかという事である。
そして、少なくとも
漢字自体も単純なものではないのかと私は疑う。
そこで、他にひらがなにした理由も考えにく
いので。無くなるのを読んで、親しみやすく
すればよいかとひらがなに変えているように私
には見えるが。その行為は、杞憂なのかもしれ
ないと、私は疑っているのである。
以上を精密に議論をするとすればきりが無い
し、それほどのものでも無いと私は考えるので。
しばらく放置すれば、そのうち「縁台将棋」に
変わるのではないかと、密かに疑っていれば、
時が解決するのでそれで良い
と考えた。以上のような思考を、私はしたとい
う事である。(2023/11/02)
福島県白河市谷地前C遺跡で古代奔人墨書土器(長さん)
今回は、福島県の旧西白川郡東村、現福島
県白河市所在の古代遺跡、谷地前C遺跡で
奈良平安期の土器に、「奔人」のようにも
見える、墨書きが検出されているとの旨の
紹介である。
「俺の物」という意味の「吾人」と読まれ
ている
ようである。
遺物の写真がweb上に公開されていて、
発掘報告書に載っている。発掘報告書が、
奈良文化財研究所発掘報告書データベース
全国遺跡報告総覧に登録・公開されている。
pdfファイル名は、以下の通りである。
23504_1_母畑地区遺跡発掘調査報告.pdf
発掘報告書の名称は以下の通りである。
福島県文化財調査報告書第85集
母畑地区遺跡発掘調査報告Ⅴ;西原遺跡・
佐平林遺跡(Ⅶ、Ⅷ区)・谷地前C遺跡、
西暦1980年3月、福島県教育委員会。
遺跡の場所は、発掘報告書第299ペー
ジ付近の「第4編谷地前C遺跡」の題字
ページの下部によると次の通りである。
西白河郡東村大字上野出島字谷地前。水郡
線里白石駅の、西2km程度の地点のよう
であり、現在白河市である。古代の律令村
と見られているようである。
同じく遺物が出土したのは、同ページに
よると、西暦1979年前後の事のようで
ある。
遺物の成立年代は、遺物は第27号住居
跡から出土した杯型の土器であり、発掘
報告書の第340ページ及び、第436
ページ付近の記載から、奈良時代中期の、
8世紀半ばと考えられているように私には
読み取れる。
遺物の写真は、発掘報告書写真図版第
75:”第27・30号住居跡出土土師器”
の最上段右に在り、そのページの第2番と
ナンバリングされている。
発掘報告書第338ページ付近によると、
「吾人」と釈文されているようである。

上図のように、確かに「俺の物」の意味
の「吾人」のようであるが字が整っていて
まじめに書いている事は明らかだが、問題
の杯の所有者を、本当に識別する気持ちが
有るのかどうかが謎
である。
酋長格の人間が、付近の人間に対し暗に、
亡くなったら自分を奉じろとの意図で書き、
「現世の奉人」との意味なのかもしれない。
現代では「吾」は「自分」の意味だが、
奈良時代には「奉人」の生前の人間の意味
だったのかもしれないと、私は疑う。宗教
か呪い活動に使うのであろう。付近からは、
病気の祈祷用と見られる、「足」の異字体
の掛かれた土器も、共出土しているらしい。
(2023/11/01)
県白河市所在の古代遺跡、谷地前C遺跡で
奈良平安期の土器に、「奔人」のようにも
見える、墨書きが検出されているとの旨の
紹介である。
「俺の物」という意味の「吾人」と読まれ
ている
ようである。
遺物の写真がweb上に公開されていて、
発掘報告書に載っている。発掘報告書が、
奈良文化財研究所発掘報告書データベース
全国遺跡報告総覧に登録・公開されている。
pdfファイル名は、以下の通りである。
23504_1_母畑地区遺跡発掘調査報告.pdf
発掘報告書の名称は以下の通りである。
福島県文化財調査報告書第85集
母畑地区遺跡発掘調査報告Ⅴ;西原遺跡・
佐平林遺跡(Ⅶ、Ⅷ区)・谷地前C遺跡、
西暦1980年3月、福島県教育委員会。
遺跡の場所は、発掘報告書第299ペー
ジ付近の「第4編谷地前C遺跡」の題字
ページの下部によると次の通りである。
西白河郡東村大字上野出島字谷地前。水郡
線里白石駅の、西2km程度の地点のよう
であり、現在白河市である。古代の律令村
と見られているようである。
同じく遺物が出土したのは、同ページに
よると、西暦1979年前後の事のようで
ある。
遺物の成立年代は、遺物は第27号住居
跡から出土した杯型の土器であり、発掘
報告書の第340ページ及び、第436
ページ付近の記載から、奈良時代中期の、
8世紀半ばと考えられているように私には
読み取れる。
遺物の写真は、発掘報告書写真図版第
75:”第27・30号住居跡出土土師器”
の最上段右に在り、そのページの第2番と
ナンバリングされている。
発掘報告書第338ページ付近によると、
「吾人」と釈文されているようである。

上図のように、確かに「俺の物」の意味
の「吾人」のようであるが字が整っていて
まじめに書いている事は明らかだが、問題
の杯の所有者を、本当に識別する気持ちが
有るのかどうかが謎
である。
酋長格の人間が、付近の人間に対し暗に、
亡くなったら自分を奉じろとの意図で書き、
「現世の奉人」との意味なのかもしれない。
現代では「吾」は「自分」の意味だが、
奈良時代には「奉人」の生前の人間の意味
だったのかもしれないと、私は疑う。宗教
か呪い活動に使うのであろう。付近からは、
病気の祈祷用と見られる、「足」の異字体
の掛かれた土器も、共出土しているらしい。
(2023/11/01)







