超奔王の着手合否判断。簡易方位角法過誤ケース残り2つ(長さん)
直近、途中駒1の4と途中駒3の5のケースについて、
それ以遠の3の7の駒を完全に隠すかどうか、一例では、
0の0が▲5八位置だったとして、3の7の▲2一桂馬
が▲4四歩兵と△2三歩兵の存在下で初期▲5八位置
超奔王で直射するのかという問題を、2円の共通内接線
の幾何学を使ったY切片計算で判断する例を示した。
簡易方位角法で、厳密な角度の順序が逆転する4例の
うちの一つであった。このうち他の例であるが、2駒の
隙間が、無限小になる(0の5)と(1の2)の間の穴
の有無の場合も、別の記事で示している。
今回は今述べた2例同様、超奔王が途中2駒の間を突
き抜けて、向こうの駒を取れるかどうかを判定する手法
で、簡易方位角計算では逆転する、残りの2例について、
幾何学でY切片の符号から、厳密に判断する計算をした
ので、以下に結果を、1の4と3の5で、3の7駒が
取れるかどうかの問題と同様に、計算の過程について説
明する。
まず、0の4と2の7が有っても、0の0から2の8
の駒が超奔王には直射しているのかどうかという問題が
ある。厳密計算で、合法(穴有り/突き抜ける)を説明
する。この例は、超奔王を自陣最下段に落として相手陣
最奥を攻める手で、実戦では余り現れ難いとみられる。
以下の図のように、途中駒を水平に寝かせると、共通
接線の傾きは、√(2/11)になる。
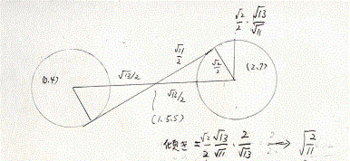
そこで三角関数の正接の加法定理の式は次のようになる。
(3/2)+√(2/11)/1-{(3/2)×√(2/11)}
分子分母に、1+{(3/2)×√(2/11)}を掛け
て、通常通り有理化する。
分子=(3/2)+√(2/11)+(9/4)×√(2/11)+(3/2)×(2×11)
=(3/2)×(13/11)+(13/4)√(2/11)
分母=1-(9/4)×(2/11)=13/22
より、最初の式は
=(22/13)×{(3/2)×(13/11)+(13/4)√(2/11)}
=3+(11/2)×√(2/11)=3+(11/2)×√(2×11)/11
=3+√22/2<3+√25/2=3+2.5=5.5
となり、X=0でY切片はプラスになるから合法である。
こちらは、√22<√25を使うので、直近で示した、
途中駒1の4と途中駒3の5のケースと同じような感じ
で、この0の4と2の7駒のケースは証明の調子が良い。
次は、0の0から見て、4の3位置駒と7の3位置駒
で8の4の駒を隠すかどうか。つまり例えば自陣右香車
初期位置0の0の超奔王から見て8の4位置の初期位置
の相手玉将の直射が、自陣右金前中段位置の4の3位置
の歩兵と、相手元の左金前に置かれた、7の3位置の、
相手の防御駒で例えば、邪魔になるかどうかという、こ
ちらも簡易方位角計算で、「非合法」への逆転例である。
このケースも自陣最下段位置から、相手陣最奥を超奔王
で攻める局面が、実戦では出難いので、現れる頻度は、
比較的レアーとみられる。
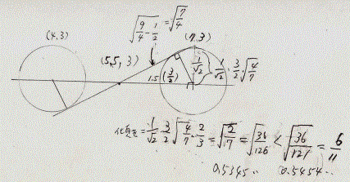
こちらは、上図中に傾き計算を入れた。間途中2駒が、
元々水平配置で傾き0なので、共通内接線の傾きだけで、
Y切片の傾きが決まる、特殊なケースである。
傾きが3/5.5以下なら合法なのだが、答えが
√(2/7)と出て本ブログの管理人などは3/5.5
と比較をどうしようかと、焦りを引き起こす。一応上図
でネタバレにしてしまったが、3/5.5は分子分母を
2倍にしてから、平方根表現に直す。つまり√記号の中
に2乗して数値を入れる。
他方、√(2/7)には、いま”2乗化”で求めた
√(36/121)となるY切片0となる場合の傾き値
に合わせる目的で、
(2/7)の分子・分母に√18を掛け√(36/126)
にする。
そうすると、このケースは分子では無く
分母同士の比較で大小が判る。
つまり、計算のめんどうさでは無くて、
どうしたら良いのか気がつくのに、手間が掛かる
という点で、方位角比較に比べて、楽かどうかが謎にな
るという例に、たまたまなっているようである。
この例に関しては、
y切片符号自体の計算が、かなり楽なので、0になる場
合との傾き値の比較方法で、考え込む時間が幾らか有っ
ても、それを出すまでの計算の簡単さが救いになる例
だろう。
以上から「『途中2駒から、第3のターゲット駒が、
取れるかどうか』の合否は、方位角比較方法によるが、
幾何学的に厳密解が出せる場合は、そちらを優先する」
という以前の提案のような表現にするしか、今の所無い。
そしてそのようにして、
玉虫色のルールで行くしか無く、後半に示した最後の比
較でつまづく例が、どの程度有るかは良く判らない。
ので、いまのところルールがこれで、問題が皆無かどう
かも実際は微妙で、個人的に私にはよく判らない。棋士
の数学能力を、現実に調査し無いと判らないほど曖昧で
あると結論出来る。以上のように本ブログの管理人には、
認識された。(2023/11/09)
それ以遠の3の7の駒を完全に隠すかどうか、一例では、
0の0が▲5八位置だったとして、3の7の▲2一桂馬
が▲4四歩兵と△2三歩兵の存在下で初期▲5八位置
超奔王で直射するのかという問題を、2円の共通内接線
の幾何学を使ったY切片計算で判断する例を示した。
簡易方位角法で、厳密な角度の順序が逆転する4例の
うちの一つであった。このうち他の例であるが、2駒の
隙間が、無限小になる(0の5)と(1の2)の間の穴
の有無の場合も、別の記事で示している。
今回は今述べた2例同様、超奔王が途中2駒の間を突
き抜けて、向こうの駒を取れるかどうかを判定する手法
で、簡易方位角計算では逆転する、残りの2例について、
幾何学でY切片の符号から、厳密に判断する計算をした
ので、以下に結果を、1の4と3の5で、3の7駒が
取れるかどうかの問題と同様に、計算の過程について説
明する。
まず、0の4と2の7が有っても、0の0から2の8
の駒が超奔王には直射しているのかどうかという問題が
ある。厳密計算で、合法(穴有り/突き抜ける)を説明
する。この例は、超奔王を自陣最下段に落として相手陣
最奥を攻める手で、実戦では余り現れ難いとみられる。
以下の図のように、途中駒を水平に寝かせると、共通
接線の傾きは、√(2/11)になる。
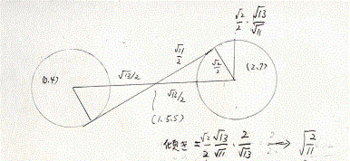
そこで三角関数の正接の加法定理の式は次のようになる。
(3/2)+√(2/11)/1-{(3/2)×√(2/11)}
分子分母に、1+{(3/2)×√(2/11)}を掛け
て、通常通り有理化する。
分子=(3/2)+√(2/11)+(9/4)×√(2/11)+(3/2)×(2×11)
=(3/2)×(13/11)+(13/4)√(2/11)
分母=1-(9/4)×(2/11)=13/22
より、最初の式は
=(22/13)×{(3/2)×(13/11)+(13/4)√(2/11)}
=3+(11/2)×√(2/11)=3+(11/2)×√(2×11)/11
=3+√22/2<3+√25/2=3+2.5=5.5
となり、X=0でY切片はプラスになるから合法である。
こちらは、√22<√25を使うので、直近で示した、
途中駒1の4と途中駒3の5のケースと同じような感じ
で、この0の4と2の7駒のケースは証明の調子が良い。
次は、0の0から見て、4の3位置駒と7の3位置駒
で8の4の駒を隠すかどうか。つまり例えば自陣右香車
初期位置0の0の超奔王から見て8の4位置の初期位置
の相手玉将の直射が、自陣右金前中段位置の4の3位置
の歩兵と、相手元の左金前に置かれた、7の3位置の、
相手の防御駒で例えば、邪魔になるかどうかという、こ
ちらも簡易方位角計算で、「非合法」への逆転例である。
このケースも自陣最下段位置から、相手陣最奥を超奔王
で攻める局面が、実戦では出難いので、現れる頻度は、
比較的レアーとみられる。
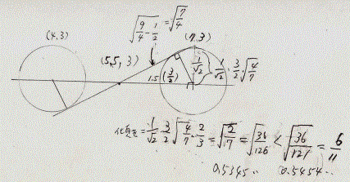
こちらは、上図中に傾き計算を入れた。間途中2駒が、
元々水平配置で傾き0なので、共通内接線の傾きだけで、
Y切片の傾きが決まる、特殊なケースである。
傾きが3/5.5以下なら合法なのだが、答えが
√(2/7)と出て本ブログの管理人などは3/5.5
と比較をどうしようかと、焦りを引き起こす。一応上図
でネタバレにしてしまったが、3/5.5は分子分母を
2倍にしてから、平方根表現に直す。つまり√記号の中
に2乗して数値を入れる。
他方、√(2/7)には、いま”2乗化”で求めた
√(36/121)となるY切片0となる場合の傾き値
に合わせる目的で、
(2/7)の分子・分母に√18を掛け√(36/126)
にする。
そうすると、このケースは分子では無く
分母同士の比較で大小が判る。
つまり、計算のめんどうさでは無くて、
どうしたら良いのか気がつくのに、手間が掛かる
という点で、方位角比較に比べて、楽かどうかが謎にな
るという例に、たまたまなっているようである。
この例に関しては、
y切片符号自体の計算が、かなり楽なので、0になる場
合との傾き値の比較方法で、考え込む時間が幾らか有っ
ても、それを出すまでの計算の簡単さが救いになる例
だろう。
以上から「『途中2駒から、第3のターゲット駒が、
取れるかどうか』の合否は、方位角比較方法によるが、
幾何学的に厳密解が出せる場合は、そちらを優先する」
という以前の提案のような表現にするしか、今の所無い。
そしてそのようにして、
玉虫色のルールで行くしか無く、後半に示した最後の比
較でつまづく例が、どの程度有るかは良く判らない。
ので、いまのところルールがこれで、問題が皆無かどう
かも実際は微妙で、個人的に私にはよく判らない。棋士
の数学能力を、現実に調査し無いと判らないほど曖昧で
あると結論出来る。以上のように本ブログの管理人には、
認識された。(2023/11/09)







