2円の共通内接線を、幾何学で解いてみる(長さん)
今回は、数学の代数で2次方程式の根の公式で
答えを出した問題を、三角関数正接(Tan)
の加法定理を使い、かつ、代数ではなく幾何学
的に、図をイメージして解き、暗算が出来ない
かどうかを、チェックしたという話題である。
問題は既に本ブログで話題にした、半径が
1/√2で等しい2円の共通内接線の、傾きや、
y切片を求め、前記2円は排除円だとして、2
つの駒の隙間から、第3の取りたい相手の駒を、
どんな方向にも走れる超奔王という、仮想の駒
で取る手が、合法か、非合法かという判別を
目的としてものである。
意外だったが、tan(α+β)=
tan(α)+tan(β)/1-tan(α)×tan(β)
の、分子分母の割り算の暗算で、頓挫してしま
うという事が判った。
最後のあと一歩の所までは、
方位角の比較暗算よりも、図形がイメージ出来
れば、むしろ暗算の演算は早い
ようである。代数的に2円の内接線の方程式
を立てて、2次方程式の根の公式に代入する、
抽象的解き方よりは、かなり人間に、把握し
易くなる。
例として、(1,4)と(3,5)の駒で、
(3,7)の駒が隠れるかという問題で以下
に、今回テストしたやり方を説明する。
自駒金将前の歩兵駒を、取り捨ての位置まで
上げ、相手の桂馬前の歩兵と、上げた取り捨
て直前味方歩兵の2駒で、相手陣で初期位置
に居る桂馬位置の駒が、味方の超奔王で直射
するかどうかという例で示される問題である。
以前PCで(1,4)と(3,5)方位角
の比較をした結果から、略算で非合法になる
のに、厳密に角度を計算すると合法で、桂馬
位置の駒は見えているという事を示した、同
様な、精密/略算反転の例のうちの、一つで
ある。
このケース、人間には頭の中で、本来下記
のように回転させて、2円の中心を結ぶ線が、
水平になり、円中心同士の距離が√5である
という幾何学図は、公式から代数方程式を作
らなくても本来は、描けるはずである。
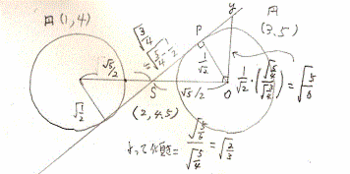
すると、図に書き込んだようなプロセスで、
円と円を結んだ線に対し、問題にしている2
円の共通内接線のうちの1本の傾きは、+
√2/3であると出せる。
ポイントは、垂線と円の中心のなす角と、
座標軸のxy軸のなす角は、共に垂直なので、
⊿OpSと⊿yOSとは相似であり、
Oy=Op×OS/Sp
のはずだという事である。そして
Sp=√(OSの2乗-Opの2乗)
である。傾きはSp/OSである。
そもそもy切片は、
2円の中点の座標(2,4.5)から、
4.5-傾き×2で簡単に出せる
ので、傾きが2.25以下ならy切片が
プラスになり、穴が見えてくる事までは、
幾何学イメージが出来ていれば頭の中で簡単
に思い浮かべる事が出来る。
ところが、その傾きだが、このケースには、
三角関数の正接の加法定理の公式:
tan(α+β)=
tan(α)+tan(β)/1-tan(α)×tan(β)
に代入し、求めようとすると、ちなみに
√(2/3)=2.44949/3=0.816・・
は、√6が「似よ良く良く」で暗算で出せ、
1/2+√(2/3)/1-(1/2×√2/3)
≒1.316・・/(1-0.408)
=1.316・・/0.592
となるのだが。
この1.316/0.592が2.25
より大きいのかどうか電卓が有れば2.22
前後で小さいと、一瞬で出るのだが、
暗算では、かなり面倒だと、私は疑う
のである。
以上1例だけだが。他でも正接(Tan)
の加法定理公式に代入時の割り算が、現実に
は暗算で、ネックになるのではないかと、私
は疑う。
本当に惜しいところだが、以上の点で同じ
半径円の共通内接線のy切片の計算よりも、
以前に示した方位角同士の比較計算の方が、
やはり、少しだけ勝っている
ように、私には依然として結論された。
代数計算は、円座標が実数で大きさがまちま
ちのときに、威力を発揮するが、同大きさ円
で中心座標が整数の如くに規則正しい時には、
幾何学図形を書いた方が、求め易いような気
がしたので、以上追加で、今回報告した次第
である。(2023/11/07)
答えを出した問題を、三角関数正接(Tan)
の加法定理を使い、かつ、代数ではなく幾何学
的に、図をイメージして解き、暗算が出来ない
かどうかを、チェックしたという話題である。
問題は既に本ブログで話題にした、半径が
1/√2で等しい2円の共通内接線の、傾きや、
y切片を求め、前記2円は排除円だとして、2
つの駒の隙間から、第3の取りたい相手の駒を、
どんな方向にも走れる超奔王という、仮想の駒
で取る手が、合法か、非合法かという判別を
目的としてものである。
意外だったが、tan(α+β)=
tan(α)+tan(β)/1-tan(α)×tan(β)
の、分子分母の割り算の暗算で、頓挫してしま
うという事が判った。
最後のあと一歩の所までは、
方位角の比較暗算よりも、図形がイメージ出来
れば、むしろ暗算の演算は早い
ようである。代数的に2円の内接線の方程式
を立てて、2次方程式の根の公式に代入する、
抽象的解き方よりは、かなり人間に、把握し
易くなる。
例として、(1,4)と(3,5)の駒で、
(3,7)の駒が隠れるかという問題で以下
に、今回テストしたやり方を説明する。
自駒金将前の歩兵駒を、取り捨ての位置まで
上げ、相手の桂馬前の歩兵と、上げた取り捨
て直前味方歩兵の2駒で、相手陣で初期位置
に居る桂馬位置の駒が、味方の超奔王で直射
するかどうかという例で示される問題である。
以前PCで(1,4)と(3,5)方位角
の比較をした結果から、略算で非合法になる
のに、厳密に角度を計算すると合法で、桂馬
位置の駒は見えているという事を示した、同
様な、精密/略算反転の例のうちの、一つで
ある。
このケース、人間には頭の中で、本来下記
のように回転させて、2円の中心を結ぶ線が、
水平になり、円中心同士の距離が√5である
という幾何学図は、公式から代数方程式を作
らなくても本来は、描けるはずである。

すると、図に書き込んだようなプロセスで、
円と円を結んだ線に対し、問題にしている2
円の共通内接線のうちの1本の傾きは、+
√2/3であると出せる。
ポイントは、垂線と円の中心のなす角と、
座標軸のxy軸のなす角は、共に垂直なので、
⊿OpSと⊿yOSとは相似であり、
Oy=Op×OS/Sp
のはずだという事である。そして
Sp=√(OSの2乗-Opの2乗)
である。傾きはSp/OSである。
そもそもy切片は、
2円の中点の座標(2,4.5)から、
4.5-傾き×2で簡単に出せる
ので、傾きが2.25以下ならy切片が
プラスになり、穴が見えてくる事までは、
幾何学イメージが出来ていれば頭の中で簡単
に思い浮かべる事が出来る。
ところが、その傾きだが、このケースには、
三角関数の正接の加法定理の公式:
tan(α+β)=
tan(α)+tan(β)/1-tan(α)×tan(β)
に代入し、求めようとすると、ちなみに
√(2/3)=2.44949/3=0.816・・
は、√6が「似よ良く良く」で暗算で出せ、
1/2+√(2/3)/1-(1/2×√2/3)
≒1.316・・/(1-0.408)
=1.316・・/0.592
となるのだが。
この1.316/0.592が2.25
より大きいのかどうか電卓が有れば2.22
前後で小さいと、一瞬で出るのだが、
暗算では、かなり面倒だと、私は疑う
のである。
以上1例だけだが。他でも正接(Tan)
の加法定理公式に代入時の割り算が、現実に
は暗算で、ネックになるのではないかと、私
は疑う。
本当に惜しいところだが、以上の点で同じ
半径円の共通内接線のy切片の計算よりも、
以前に示した方位角同士の比較計算の方が、
やはり、少しだけ勝っている
ように、私には依然として結論された。
代数計算は、円座標が実数で大きさがまちま
ちのときに、威力を発揮するが、同大きさ円
で中心座標が整数の如くに規則正しい時には、
幾何学図形を書いた方が、求め易いような気
がしたので、以上追加で、今回報告した次第
である。(2023/11/07)







