二中歴の記載は将棋が主で大将棋は従(長さん)
これもまた、本ブログの管理人が以前には
読み落とししていたという内容である。
二中歴の記載より、著者は日本の将棋に
関して、大将棋が西暦1200年頃の標準
では無いと、明らかに思っていた事が判る。
もしそうで無いならば将棋の説明で、
大将棋を先に書き、「簡易版として、将棋
がある」と記載するはず
である。
大将棋がどうして従だったかは、著者が
平安小将棋の棋士であったからであると、
強弁出来無くもないのであるが。小を付け
ないところを見ても、文面の通り(平安小)
将棋がいわゆる、日本の将棋であり、それ
とは別に、大将棋があると見られたので、
そのように書いて、挙中歴(ほぼ手帳だろ
う)としておかしく無かった可能性の方が、
少なくとも高いのであろう。
この事から、平安小将棋が名人を出すよ
うなゲームではなくて、子供の遊戯として
日本に現れ、その後結果的には、大人が指
しておかしく無い体裁の、大将棋を作ろう
とした形跡が明らかに有るように私見する。
平安小将棋の発生ないし伝来は、子供用
だった事を示唆しているのでは無いのか。
とすると船で外国から、大枚をはたいて
伝来させるのに、下々の子供の為とわざわ
ざというのも、無いとは言い切れないであ
ろうが。当時として可能性が、余り高くは、
無いように思える。
つまり、
もともと日本の将棋は発生時皇族の子息用
だったとするならば、自然伝来だとすると、
少なくとも囲碁を盛んに指す、ゲームの出
来に目の肥えた国で、子供用だけ伝えて、
幻の大理国大将棋を無視する点の不自然さ
は消えるように、私には思えるという事で
ある。
そして親王のうち、跳びぬけて存在に期
待の掛かった人物といえば、ちょうど将棋
発生のタイミングの10世紀後半から、
西暦1058年迄の間と絞れば、敦成親王
用に伝来というのが、最初からそれだけで、
かなり疑われて然るべきだったように、私
には思えるように反省が必要との気分に、
ここへ来て正直なって来た。(2023/10/31)
読み落とししていたという内容である。
二中歴の記載より、著者は日本の将棋に
関して、大将棋が西暦1200年頃の標準
では無いと、明らかに思っていた事が判る。
もしそうで無いならば将棋の説明で、
大将棋を先に書き、「簡易版として、将棋
がある」と記載するはず
である。
大将棋がどうして従だったかは、著者が
平安小将棋の棋士であったからであると、
強弁出来無くもないのであるが。小を付け
ないところを見ても、文面の通り(平安小)
将棋がいわゆる、日本の将棋であり、それ
とは別に、大将棋があると見られたので、
そのように書いて、挙中歴(ほぼ手帳だろ
う)としておかしく無かった可能性の方が、
少なくとも高いのであろう。
この事から、平安小将棋が名人を出すよ
うなゲームではなくて、子供の遊戯として
日本に現れ、その後結果的には、大人が指
しておかしく無い体裁の、大将棋を作ろう
とした形跡が明らかに有るように私見する。
平安小将棋の発生ないし伝来は、子供用
だった事を示唆しているのでは無いのか。
とすると船で外国から、大枚をはたいて
伝来させるのに、下々の子供の為とわざわ
ざというのも、無いとは言い切れないであ
ろうが。当時として可能性が、余り高くは、
無いように思える。
つまり、
もともと日本の将棋は発生時皇族の子息用
だったとするならば、自然伝来だとすると、
少なくとも囲碁を盛んに指す、ゲームの出
来に目の肥えた国で、子供用だけ伝えて、
幻の大理国大将棋を無視する点の不自然さ
は消えるように、私には思えるという事で
ある。
そして親王のうち、跳びぬけて存在に期
待の掛かった人物といえば、ちょうど将棋
発生のタイミングの10世紀後半から、
西暦1058年迄の間と絞れば、敦成親王
用に伝来というのが、最初からそれだけで、
かなり疑われて然るべきだったように、私
には思えるように反省が必要との気分に、
ここへ来て正直なって来た。(2023/10/31)
排除角下限・上限計算。略算が脳内計算だと再逆転するか(長さん)
既に本ブログでは、数学的問題として、
格子状に円を描いたときの、特定円から
見た、他の円の方位角という問題を、
将棋盤上に駒がある場合、走り駒がその
先に行けないという問題と関連して論じ
た。この場合円は過密であり、充填する
と、特定円中心から見て、縦横4隣接円
で斜めに、無限小の隙間が空くだけとい
う、角行ルールに即した条件である。
特定円を0の0として、他の各円の、
接線の方位角を、幾何学と、暗算の為の
略算でする、両方法を示し、その差を
論じてきた。その結果、本ブログで示し
た略算は、将棋の”禁手を指す”に対応
して、絶対避けるぺきな為、円半径を、
180/√2π=40.5・・より大き
な42°にして、暗算もやり易くした為、
主としてそれが原因で、5か所結果が厳
密計算とは、不整合であった。
そのうち2つについては、暗算過程を
以前に示した。そこで今回は、残りの3
つについて、実暗算で、PCによる計算
と、状況が同じになるのかをチェックし
たので、以下に結果を紹介する。
(1)4の0駒上限と7の2の駒下限
まずは、4の0の駒の上限と7の2の
駒の下限で、はしょり略算で穴が空くか
という問題である。
簡単な4の0の上限から考える。中心
方位角は0°である。
排除円の半径は10.5°であり、
4の0の上限は10.5°である。
次に、7の2の下限について。
最初に排除円半径を計算しておく。
こういうケース、42を割る計算は、
開平の前にした方が良い。何回かこの作
業をするうち42の2乗が、
1764である事を覚えるのが必須と私
も気が付いた。
1764/53が、意外に最大の難所で
ある。3が立ち176-159=17。
174でも3しか立たず、150でも
約3である。33.3位という事である。
開平計算に入る。33.3-25=
8.3で8.3/5/2=
8.3/10=0.83だから、
√1764/53=5.83程度と出る。
次に、7の2の中心の方位角は、
55×(2/7)=16°弱である。
よって、7の2の排除円下限方位角は、
16-5.83=10.17°で、
計算が雑でも、再逆転は無い。
(2)5の3駒下限と4の1駒上限
次に、5の3の下と4の1の上で、
暗算を雑にやると穴が空かないかについ
て、考えてみる。
5の3について。
排除円の視半径は、7.20294
(難波憎し)と暗算する事になっている。
中心の方位角は、
42×(3/5)+5.5=30.7°
下限は30.7-7.20294=
23.5・・°となる。
4の1について。
排除円の視半径は、10.18(=
10.5-0.32:0.32の32
は、「渚に色」の「さに」である。)
と、暗記する事になっている。
排除円中心の方位角は55/4=
14°弱である。
排除円上限は、14+10.18=
24.18で、
計算が雑でも、穴は隠れている。
ここまでは、55/Xの計算が雑でも、
たまたまその誤差が円重なりが増える
ようになったので、誤差が利かないケース
である。
(3)4の3駒下限と7の3駒上限
次に、4の3と7の3で、穴が空かな
いかどうかについて、確認する。
まず簡単な4の3について。
排除円はピタゴラスの三角形で接線長
さが5であるから8.4°となる。
次に方位角は42×(3/4)+5.5
=37°。排除円下限は28.6°である。
次に難物の7の3について。
排除円視半径は、
1764/58=は3が立ち、24/58
は、0.4強である。
√30.4は、5.4/10=0.54
であるから、5.54程度とみられる。
次に中心点方位角は、55×(3/7)
=24°弱であり、排除円上限は、
29.54°であり、
このケースも、穴は開かない。
このケースも55/Xの計算が雑な事で、
かえって助かっているケースである。
以上で、少なくとも本来人間の頭の中で
するはずの「雑な計算」をPCでした事に
よる影響は、微妙なケースの一部について
は、存在し無い事が判った。
ただし厳格計算で、逆転したケースだけ
ピックアップして、大丈夫かというと私に
は自信が無いが、きりが無いのでこのへん
で止めた。
このタイプの計算練習をして私が悟った
ポイントは、排除円半径を計算するときに、
42の2乗が1764になる事は暗記して
おいて、
割算で、割る数の有効数字が増えないよう
にして暗算を楽にするという点が最も大切
という事である。つまり、開平計算は、大
きいところを暗記してしまい、計算は最大
で√48前後までしか無ければ、略暗算は、
前記のような割り算よりは、むしろ楽だっ
たのである。(2023/10/30)
格子状に円を描いたときの、特定円から
見た、他の円の方位角という問題を、
将棋盤上に駒がある場合、走り駒がその
先に行けないという問題と関連して論じ
た。この場合円は過密であり、充填する
と、特定円中心から見て、縦横4隣接円
で斜めに、無限小の隙間が空くだけとい
う、角行ルールに即した条件である。
特定円を0の0として、他の各円の、
接線の方位角を、幾何学と、暗算の為の
略算でする、両方法を示し、その差を
論じてきた。その結果、本ブログで示し
た略算は、将棋の”禁手を指す”に対応
して、絶対避けるぺきな為、円半径を、
180/√2π=40.5・・より大き
な42°にして、暗算もやり易くした為、
主としてそれが原因で、5か所結果が厳
密計算とは、不整合であった。
そのうち2つについては、暗算過程を
以前に示した。そこで今回は、残りの3
つについて、実暗算で、PCによる計算
と、状況が同じになるのかをチェックし
たので、以下に結果を紹介する。
(1)4の0駒上限と7の2の駒下限
まずは、4の0の駒の上限と7の2の
駒の下限で、はしょり略算で穴が空くか
という問題である。
簡単な4の0の上限から考える。中心
方位角は0°である。
排除円の半径は10.5°であり、
4の0の上限は10.5°である。
次に、7の2の下限について。
最初に排除円半径を計算しておく。
こういうケース、42を割る計算は、
開平の前にした方が良い。何回かこの作
業をするうち42の2乗が、
1764である事を覚えるのが必須と私
も気が付いた。
1764/53が、意外に最大の難所で
ある。3が立ち176-159=17。
174でも3しか立たず、150でも
約3である。33.3位という事である。
開平計算に入る。33.3-25=
8.3で8.3/5/2=
8.3/10=0.83だから、
√1764/53=5.83程度と出る。
次に、7の2の中心の方位角は、
55×(2/7)=16°弱である。
よって、7の2の排除円下限方位角は、
16-5.83=10.17°で、
計算が雑でも、再逆転は無い。
(2)5の3駒下限と4の1駒上限
次に、5の3の下と4の1の上で、
暗算を雑にやると穴が空かないかについ
て、考えてみる。
5の3について。
排除円の視半径は、7.20294
(難波憎し)と暗算する事になっている。
中心の方位角は、
42×(3/5)+5.5=30.7°
下限は30.7-7.20294=
23.5・・°となる。
4の1について。
排除円の視半径は、10.18(=
10.5-0.32:0.32の32
は、「渚に色」の「さに」である。)
と、暗記する事になっている。
排除円中心の方位角は55/4=
14°弱である。
排除円上限は、14+10.18=
24.18で、
計算が雑でも、穴は隠れている。
ここまでは、55/Xの計算が雑でも、
たまたまその誤差が円重なりが増える
ようになったので、誤差が利かないケース
である。
(3)4の3駒下限と7の3駒上限
次に、4の3と7の3で、穴が空かな
いかどうかについて、確認する。
まず簡単な4の3について。
排除円はピタゴラスの三角形で接線長
さが5であるから8.4°となる。
次に方位角は42×(3/4)+5.5
=37°。排除円下限は28.6°である。
次に難物の7の3について。
排除円視半径は、
1764/58=は3が立ち、24/58
は、0.4強である。
√30.4は、5.4/10=0.54
であるから、5.54程度とみられる。
次に中心点方位角は、55×(3/7)
=24°弱であり、排除円上限は、
29.54°であり、
このケースも、穴は開かない。
このケースも55/Xの計算が雑な事で、
かえって助かっているケースである。
以上で、少なくとも本来人間の頭の中で
するはずの「雑な計算」をPCでした事に
よる影響は、微妙なケースの一部について
は、存在し無い事が判った。
ただし厳格計算で、逆転したケースだけ
ピックアップして、大丈夫かというと私に
は自信が無いが、きりが無いのでこのへん
で止めた。
このタイプの計算練習をして私が悟った
ポイントは、排除円半径を計算するときに、
42の2乗が1764になる事は暗記して
おいて、
割算で、割る数の有効数字が増えないよう
にして暗算を楽にするという点が最も大切
という事である。つまり、開平計算は、大
きいところを暗記してしまい、計算は最大
で√48前後までしか無ければ、略暗算は、
前記のような割り算よりは、むしろ楽だっ
たのである。(2023/10/30)
なぜ2の1の駒の下内側と5の0の駒の上外側角一致(長さん)
今回は、幾何学の話題であり、将棋の升目座標で、
2の1の駒の下内側縁視線と5の0の駒の上外側
縁視線とが、2円の共通外接線になり、完全に
重なるのか。その理由を、数学で考察する。
自陣玉将(5九)の位置から見て、前升目5八
や横升目4九・6九に「途中の駒」を置くと視半
径45°に見えるときに、玉先の歩兵が突き捨て
直前になる5四の位置に居るとき、金将先の歩兵
4七か6七かとで、無限に小さい隙間を作る問題
である等と、このケースには例示する事が出来る。
整数の性質で、50-1=7の2乗、
10-1=3の2乗で、たまたまある為だ
と、私には理解出来た。
排除円は長さを升目単位にとると、1/√2だ
が、以下の議論で、全体として長さの単位を
√2倍して、将棋盤の1升目の距離は√2で
あり、排除円が1であるとして示す。その方が、
間違い難いようである。
そもそも、2の1と5の0に外接線を漠然と引
くと、繰り返すと排除円半径を1とすると、
2の1と5の0の中心間距離は、√2×√10
=2√5である。従って、下図より明らかに、
外接線の、接点間距離は2×2=4である。
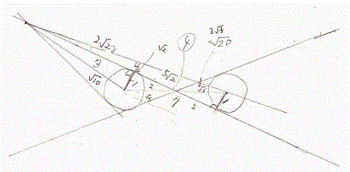
そこで、こんどは超奔王の位置から、おのおの
に接線を引く。
2の1については、超奔王の0の0点から
円の中心までの距離が図のごとくに√2×√5
で√10であり、排除円が半径1であるから、
接点までの距離は、√9で3ちょうどである。
他方5の0については、同じく超奔王の0の0
点から円の中心までの距離が図のごとくに、
√2×5で√50であり、排除円が半径1である
から、接点までの距離は、√49で7ちょうどで
ある。
つまり、0の0点からの接点距離差は7-3
で4であり、つまり、0の0の点、2つの円の接
点は、直線上に並んでいなければならない。よっ
て、引き方を替えても、同じ線である事を明らか
に示している。
どうやら、このケースは、数論・幾何学が得意
な棋士には、近似計算に誤差がある事は、直ぐに
見破られてしまいそうである。よって、方位角
45°で、共通接線が1本にマトまるケース同様、
幾何学的に特殊なケースは、厳密な議論を優先
して、このケースも、合法手とした方が良い。
以上のように結論されるように、私には思われた。
(2023/10/29)
2の1の駒の下内側縁視線と5の0の駒の上外側
縁視線とが、2円の共通外接線になり、完全に
重なるのか。その理由を、数学で考察する。
自陣玉将(5九)の位置から見て、前升目5八
や横升目4九・6九に「途中の駒」を置くと視半
径45°に見えるときに、玉先の歩兵が突き捨て
直前になる5四の位置に居るとき、金将先の歩兵
4七か6七かとで、無限に小さい隙間を作る問題
である等と、このケースには例示する事が出来る。
整数の性質で、50-1=7の2乗、
10-1=3の2乗で、たまたまある為だ
と、私には理解出来た。
排除円は長さを升目単位にとると、1/√2だ
が、以下の議論で、全体として長さの単位を
√2倍して、将棋盤の1升目の距離は√2で
あり、排除円が1であるとして示す。その方が、
間違い難いようである。
そもそも、2の1と5の0に外接線を漠然と引
くと、繰り返すと排除円半径を1とすると、
2の1と5の0の中心間距離は、√2×√10
=2√5である。従って、下図より明らかに、
外接線の、接点間距離は2×2=4である。

そこで、こんどは超奔王の位置から、おのおの
に接線を引く。
2の1については、超奔王の0の0点から
円の中心までの距離が図のごとくに√2×√5
で√10であり、排除円が半径1であるから、
接点までの距離は、√9で3ちょうどである。
他方5の0については、同じく超奔王の0の0
点から円の中心までの距離が図のごとくに、
√2×5で√50であり、排除円が半径1である
から、接点までの距離は、√49で7ちょうどで
ある。
つまり、0の0点からの接点距離差は7-3
で4であり、つまり、0の0の点、2つの円の接
点は、直線上に並んでいなければならない。よっ
て、引き方を替えても、同じ線である事を明らか
に示している。
どうやら、このケースは、数論・幾何学が得意
な棋士には、近似計算に誤差がある事は、直ぐに
見破られてしまいそうである。よって、方位角
45°で、共通接線が1本にマトまるケース同様、
幾何学的に特殊なケースは、厳密な議論を優先
して、このケースも、合法手とした方が良い。
以上のように結論されるように、私には思われた。
(2023/10/29)
PCプログラミングで厳密計算と暗算用略算比較(長さん)
既に述べたように、将棋駒の走りを拡張した、
アナログ全方向走りで、「途中に駒が有る場合」
の途中駒を、隣接1升目離れで視半径45°
(-δ;δ→0)の排除半径を持つ駒と定義し、
中心方位角と排除視半径を暗算で出来る程度に、
計算を近似式化し、それによって方位角範囲(上
端と下端)計算を簡略すると、厳密に三角関数や
ピタゴラスの定理を用いた場合と、合わない場合
が発生した。
特に、視半径を0の1/1の0で45°、
1の1で30°、それ以遠で42°/距離で
逆比例と近似暗算計算し、方位角はarcTan
計算を数表を用いず、
0~ほぼ0.44未満まで、55×正弦°
0.44以上~0.8未満まで42×正弦+5.5°、
0.8から1まで30×正弦+15°と
折れ線近似をして、方位角範囲(上端と下端)計算
をすると、3の0の上限よりも7の1の上限が、
前記暗算用暗算計算では、小さく出るが、厳密
に数表を使って計算すると、7の1の上限よりも
3の0の上限の方が小さく、直射して合法になる
という逆転が起こり、禁手を過剰に恐れすぎの
「ぼんやり者間違い計算」として問題になった。
他には「途中に1駒ある場合」の逆転は、無さ
そうであったが、気になる為、今回は、煩雑さも
あって、PCでプログラミングして、方位角計算
で、暗算用略算だと順位が逆転する箇所を全抽出
してみた。
以下は、以前に問題にした方位角45°の場合
の、穴を構成する駒への「全当たり」の問題を
除く、片側方位角43°付近までの、全ケースの
方位角計算の、暗算用略算と、三角関数やピタゴ
ラスの定理を用いた厳格計算の、比較プログラミ
ング例である。以下は個人的に、私には作成楽な、
いわゆるPCプログラム:日本電気㈱の昔流行の、
N88Basic(互換)で書いている。
100 CLS
200 OPEN "TEST.TXT" FOR OUTPUT AS #1
1000 OPTION BASE 0
1020 RADOODO=57.2957795
1040 HANKEI=1/SQR(2)
1100 DIM ARCGEN(8,8,2):DIM ARCRYAK(8,8,2)
1120 DIM GYO(8):DIM RETU(8)
1200 FOR I=0 TO 8:GYO(I)=I:RETU(I)=I:NEXT I
1300 DIM ARCNA$(8,8,4)
1320 DIM ARCGENL(144): DIM ARCGENN$(144):DIM ARCRYAKL(144):DIM ARCRYAKN$(144)
1400 FOR I=0 TO 8
1500 FOR J=0 TO 8
1600 ARCNA$(I,J,1)=STR$(GYO(I))+" "+STR$(RETU(J))+" 計下"
1700 ARCNA$(I,J,2)=STR$(GYO(I))+" "+STR$(RETU(J))+" 計上"
1800 ARCNA$(I,J,3)=STR$(GYO(I))+" "+STR$(RETU(J))+" 厳下"
1900 ARCNA$(I,J,4)=STR$(GYO(I))+" "+STR$(RETU(J))+" 厳上"
2000 NEXT J
2100 NEXT I
2900 '
2920 ARCRYAK(0,0,1)=225:ARCRYAK(0,0,2)=225
3000 FOR I=1 TO 8
3100 FOR J=0 TO 8
3200 IF J/I<0.44 THEN TYU=55*J/I:GOTO 4000
3300 IF (J/I>=0.44 AND J/I<0.8) THEN TYU=42*J/I+5.5:GOTO 4000
3400 IF (J/I>=0.8 AND J/I<=1) THEN TYU=30*J/I+15:GOTO 4000
3500 IF (I/J>=0.8 AND I/J<1) THEN TYU=90-(30*I/J+15):GOTO 4000
3600 IF (I/J>=0.44 AND I/J<0.8) THEN TYU=90-(42*I/J+5.5):GOTO 4000
3700 IF I/J<0.44 THEN TYU=90-(55*I/J):GOTO 4000
4000 '
4100 HAIJO=42/SQR(I*I+J*J)
4200 IF I=1 AND J=0 THEN HAIJO=45
4300 IF I=1 AND J=1 THEN HAIJO=30
4400 ARCRYAK(I,J,1)=TYU-HAIJO
4500 ARCRYAK(I,J,2)=TYU+HAIJO
4800 NEXT J
4900 NEXT I
5000 '
5002 CONT%=0
5100 FOR I=1 TO 8:FOR J=0 TO 8:FOR K=1 TO 2
5200 CONT%=CONT%+1
5300 ARCRYAKL(CONT%)=ARCRYAK(I,J,K)
5400 ARCRYAKN$(CONT%)=ARCNA$(I,J,K)
5500 NEXT K:NEXT J:NEXT I
5600 '
5700 FOR I=1 TO 8
5800 FOR J=0 TO 8
5820 TYU=RADOODO*ATN(J/I)
5900 HAIJO=RADOODO*ATN(HANKEI/SQR(I*I+J*J-0.5))
6000 ARCGEN(I,J,1)=TYU-HAIJO
6100 ARCGEN(I,J,2)=TYU+HAIJO
6200 NEXT J
6300 NEXT I
6400 '
7100 CONT%=0
7200 FOR I=1 TO 8:FOR J=0 TO 8:FOR K=1 TO 2
7300 CONT%=CONT%+1
7400 ARCGENL(CONT%)=ARCGEN(I,J,K)
7500 ARCGENN$(CONT%)=ARCNA$(I,J,K+2)
7600 NEXT K:NEXT J:NEXT I
7700 CONT%=0
7900 '
8000 FOR I=1 TO 143
8100 FOR J=I+1 TO 144
8200 IF ARCRYAKL(I)>ARCRYAKL(J) THEN SWAP ARCRYAKL(I),ARCRYAKL(J):SWAP ARCRYAKN$(I),ARCRYAKN$(J)
8400 IF ARCGENL(I)>ARCGENL(J) THEN SWAP ARCGENL(I),ARCGENL(J):SWAP ARCGENN$(I),ARCGENN$(J)
8600 NEXT J
8700 NEXT I
9000 '
9100 FOR I=1 TO 72
9200 PRINT #1, USING "##;& &;####.######;& &;####.#####";I,ARCRYAKN$(I),ARCRYAKL(I),ARCGENN$(I),ARCGENL(I)
9300 NEXT I
9320 CLOSE #1
9400 END
実行させると次のように答えが出るので、問題点
をタイピングして、抽出している。
なお以下は1行毎に、”順位、升目、限界角種類、方位角計算結果、
升目、限界角種類、方位角計算結果”を示している。
1; 1 0 計下 ; -45.000000; 1 0 厳下 ; -45.00000
2; 2 0 計下 ; -21.000000; 2 0 厳下 ; -20.70481
3; 3 0 計下 ; -14.000000; 3 0 厳下 ; -13.63302
4; 4 0 計下 ; -10.500000; 4 0 厳下 ; -10.18207
5; 5 0 計下 ; -8.400000; 5 0 厳下 ; -8.13010
6; 6 0 計下 ; -7.000000; 6 0 厳下 ; -6.76810
7; 7 0 計下 ; -6.000000; 7 0 厳下 ; -5.79764
8; 8 0 計下 ; -5.250000; 8 0 厳下 ; -5.07090
9; 8 1 計下 ; 1.665541; 8 1 厳下 ; 2.09338
10; 7 1 計下 ; 1.917446; 7 1 厳下 ; 2.39093
11; 6 1 計下 ; 2.261909; 6 1 厳下 ; 2.78673
12; 5 1 計下 ; 2.763122; 5 1 厳下 ; 3.33875
13; 4 1 計下 ; 3.563504; 4 1 厳下 ; 4.16128
14; 3 1 計下 ; 5.051767; 8 0 厳上 ; 5.07090
15; 8 0 計上 ; 5.250000; 3 1 厳下 ; 5.51398
16; 7 0 計上 ; 6.000000; 7 0 厳上 ; 5.79764
17; 6 0 計上 ; 7.000000; 6 0 厳上 ; 6.76810
18; 2 1 計下 ; 7.717029; 5 0 厳上 ; 8.13010←要注意
19; 5 0 計上 ; 8.400000; 2 1 厳下 ; 8.13010←
20; 8 2 計下 ; 8.656752; 8 2 厳下 ; 9.11713
21; 7 2 計下 ; 9.945142; 4 0 厳上 ; 10.18207←問題なし
22; 4 0 計上 ; 10.500000; 7 2 厳下 ; 10.37155←
23; 6 2 計下 ; 11.692550; 6 2 厳下 ; 12.01566
24; 8 1 計上 ; 12.084459; 8 1 厳上 ; 12.15665
25; 7 1 計上 ; 13.796840; 3 0 厳上 ; 13.63302←議論済
26; 3 0 計上 ; 14.000000; 7 1 厳上 ; 13.86927←
27; 5 2 計下 ; 14.200796; 5 2 厳下 ; 14.25632
28; 1 1 計下 ; 15.000000; 1 1 厳下 ; 15.00000
29; 8 3 計下 ; 15.709272; 8 3 厳下 ; 15.80878
30; 6 1 計上 ; 16.071424; 6 1 厳上 ; 16.13791
31; 4 2 計下 ; 17.108514; 4 2 厳下 ; 17.46762
32; 7 3 計下 ; 18.056558; 7 3 厳下 ; 17.87114
33; 8 2 計上 ; 18.843248; 8 2 厳上 ; 18.95536
34; 5 1 計上 ; 19.236878; 5 1 厳上 ; 19.28112
35; 6 3 計下 ; 20.239010; 6 3 厳下 ; 20.51431
36; 2 0 計上 ; 21.000000; 2 0 厳上 ; 20.70481
37; 7 2 計上 ; 21.483429; 7 2 厳上 ; 21.51924
38; 8 4 計下 ; 21.804257; 8 4 厳下 ; 22.03069
39; 3 2 計下 ; 21.851296; 3 2 厳下 ; 22.38014
40; 5 3 計下 ; 23.497059; 4 1 厳上 ; 23.91120←問題なし
41; 4 1 計上 ; 23.936496; 5 3 厳下 ; 23.99848←
42; 7 4 計下 ; 24.290541; 7 4 厳下 ; 24.71324
43; 6 2 計上 ; 24.974116; 6 2 厳上 ; 24.85423
44; 8 3 計上 ; 25.540728; 8 3 厳上 ; 25.30331
45; 8 5 計下 ; 27.298009; 8 5 厳下 ; 27.70685
46; 6 4 計下 ; 27.675648; 6 4 厳下 ; 28.06271
47; 4 3 計下 ; 28.600000; 7 3 厳上 ; 28.52604←問題なし
48; 7 3 計上 ; 29.086299; 4 3 厳下 ; 28.73980←
49; 5 2 計上 ; 29.799204; 5 2 厳上 ; 29.34650
50; 2 2 計下 ; 30.150758; 2 2 厳下 ; 30.52249
51; 7 5 計下 ; 30.617599; 7 5 厳下 ; 30.82267
52; 8 4 計上 ; 31.195743; 8 4 厳上 ; 31.09941
53; 3 1 計上 ; 31.614900; 3 1 厳上 ; 31.35592
54; 5 4 計下 ; 32.440702; 5 4 厳下 ; 32.31962
55; 6 3 計上 ; 32.760990; 6 3 厳上 ; 32.61580
56; 8 6 計下 ; 32.800000; 8 6 厳下 ; 32.81509
57; 6 5 計下 ; 34.622451; 6 5 厳下 ; 34.61114
58; 7 4 計上 ; 34.709459; 7 4 厳上 ; 34.77652
59; 3 3 計下 ; 35.100505; 3 3 厳下 ; 35.40593
60; 4 2 計上 ; 35.891486; 4 2 厳上 ; 35.66249
61; 7 6 計下 ; 36.158746; 7 6 厳下 ; 36.20259
62; 8 5 計上 ; 36.201991; 8 5 厳上 ; 36.30391
63; 8 7 計下 ; 37.298972; 8 7 厳下 ; 37.37185
64; 4 4 計下 ; 37.575379; 4 4 厳下 ; 37.81924
65; 5 3 計上 ; 37.902941; 5 3 厳上 ; 37.92903
66; 5 5 計下 ; 39.060303; 5 5 厳下 ; 39.26083
67; 6 4 計上 ; 39.324352; 6 4 厳上 ; 39.31742
68; 6 6 計下 ; 40.050253; 6 6 厳下 ; 40.21981
69; 7 5 計上 ; 40.382401; 7 5 厳上 ; 40.25268
70; 7 7 計下 ; 40.757359; 7 7 厳下 ; 40.90396
71; 8 6 計上 ; 41.200000; 8 6 厳上 ; 40.92470
72; 8 8 計下 ; 41.287689; 8 8 厳下 ; 41.41668
上記の結果リストから判るように、9×9升目
盤では所詮、チェックが必要な方位角計算は、
事実上この、72通りしか無いのである。
そして、右隅のコメントのように
暗算の為の略計算では5箇所、厳密計算
との間に、違いが生じている。
ただし、途中駒がターゲット駒を隠すというカテ
ゴリーの間違いは冒頭で紹介した「7の1の上限
よりも3の0の上限の方が小さい」という1箇所
だけである。
残りの4箇所は、厳密計算では角道状の穴から、
向こうの駒を突きぬいて取れるのに、略算すると、
穴が無くなるという「角道類似型間違い」だけ
である。排除円の半径を、遠方で過大に見ている
のが、差異が生じる主原因だと私は解釈する。
そのうち以下説明するケースを除く3つは、私
には将棋盤を見ても、にわかにはピンと来ない
ケースである。例えば上記のリストで40と41
の逆転については「略算だと、そういうものか」
と私なら諦める例か?
これらは、間違っていても略算結果が正しいとし
て非合法にしてしまって、問題無いのではないか
と疑われるという意味である。
残りの一つで、上記で要注意とした一番上のケー
スというのは、
初期位置の5八位置に、超奔王が最初居るとして、
超奔王先の歩兵は突き捨てる位置5四に居て、盤
面には、自陣の金将前と超奔王前の3歩だけ有っ
て残りの15個の歩兵は無いとしたときに、以前
述べたように、超奔王位置から、相手陣両金将位
置の駒はその場合にも直射するのだが、仮に味方
の玉将が、別の位置に移動済みで、一歩超奔王自
身が後退して
▲5九超奔王としても、味方の金将前3段目両歩
兵と、味方の5四位値の、突き捨て歩兵の2枚組
「途中の駒」の間に、無限小の大きさの角道型穴
が空いていて、相手陣の両金将位置駒を、その無
限小の大きさの穴で突き刺せる
のではいかと、例示されるようなケースである。
厳密計算結果は、私は大学受験のときチェック
漏れしたが、2円の共通外接線の傾きが特定の場
合のケースであるらしく、5九の奔王位置から、
共通外接線光路で、相手陣金将位置の駒が無限小
の角度で覗いているらしい。
このケースは、超奔王を1歩後退しても、相手
金将位置駒が取れるというルールが「小気味良い」
感じなので、厳密計算と無限小の次数解析(この
場合も同次の無限小だとみられる)で、いっけん
厳密計算を採用したくもなる、例外
のようにも感じる。
特に、相手が幾何学が強い棋士なら、突っ込み
が入るかもしれない。継続して、議論すべきかと
思う。
上記のNo.18と19の、2の1と5の0で、
無限小の穴を作る例だけ、そのうち円の共通接線
の幾何学で、チェックしてみようと私は考えた。
(2023/10/28)
アナログ全方向走りで、「途中に駒が有る場合」
の途中駒を、隣接1升目離れで視半径45°
(-δ;δ→0)の排除半径を持つ駒と定義し、
中心方位角と排除視半径を暗算で出来る程度に、
計算を近似式化し、それによって方位角範囲(上
端と下端)計算を簡略すると、厳密に三角関数や
ピタゴラスの定理を用いた場合と、合わない場合
が発生した。
特に、視半径を0の1/1の0で45°、
1の1で30°、それ以遠で42°/距離で
逆比例と近似暗算計算し、方位角はarcTan
計算を数表を用いず、
0~ほぼ0.44未満まで、55×正弦°
0.44以上~0.8未満まで42×正弦+5.5°、
0.8から1まで30×正弦+15°と
折れ線近似をして、方位角範囲(上端と下端)計算
をすると、3の0の上限よりも7の1の上限が、
前記暗算用暗算計算では、小さく出るが、厳密
に数表を使って計算すると、7の1の上限よりも
3の0の上限の方が小さく、直射して合法になる
という逆転が起こり、禁手を過剰に恐れすぎの
「ぼんやり者間違い計算」として問題になった。
他には「途中に1駒ある場合」の逆転は、無さ
そうであったが、気になる為、今回は、煩雑さも
あって、PCでプログラミングして、方位角計算
で、暗算用略算だと順位が逆転する箇所を全抽出
してみた。
以下は、以前に問題にした方位角45°の場合
の、穴を構成する駒への「全当たり」の問題を
除く、片側方位角43°付近までの、全ケースの
方位角計算の、暗算用略算と、三角関数やピタゴ
ラスの定理を用いた厳格計算の、比較プログラミ
ング例である。以下は個人的に、私には作成楽な、
いわゆるPCプログラム:日本電気㈱の昔流行の、
N88Basic(互換)で書いている。
100 CLS
200 OPEN "TEST.TXT" FOR OUTPUT AS #1
1000 OPTION BASE 0
1020 RADOODO=57.2957795
1040 HANKEI=1/SQR(2)
1100 DIM ARCGEN(8,8,2):DIM ARCRYAK(8,8,2)
1120 DIM GYO(8):DIM RETU(8)
1200 FOR I=0 TO 8:GYO(I)=I:RETU(I)=I:NEXT I
1300 DIM ARCNA$(8,8,4)
1320 DIM ARCGENL(144): DIM ARCGENN$(144):DIM ARCRYAKL(144):DIM ARCRYAKN$(144)
1400 FOR I=0 TO 8
1500 FOR J=0 TO 8
1600 ARCNA$(I,J,1)=STR$(GYO(I))+" "+STR$(RETU(J))+" 計下"
1700 ARCNA$(I,J,2)=STR$(GYO(I))+" "+STR$(RETU(J))+" 計上"
1800 ARCNA$(I,J,3)=STR$(GYO(I))+" "+STR$(RETU(J))+" 厳下"
1900 ARCNA$(I,J,4)=STR$(GYO(I))+" "+STR$(RETU(J))+" 厳上"
2000 NEXT J
2100 NEXT I
2900 '
2920 ARCRYAK(0,0,1)=225:ARCRYAK(0,0,2)=225
3000 FOR I=1 TO 8
3100 FOR J=0 TO 8
3200 IF J/I<0.44 THEN TYU=55*J/I:GOTO 4000
3300 IF (J/I>=0.44 AND J/I<0.8) THEN TYU=42*J/I+5.5:GOTO 4000
3400 IF (J/I>=0.8 AND J/I<=1) THEN TYU=30*J/I+15:GOTO 4000
3500 IF (I/J>=0.8 AND I/J<1) THEN TYU=90-(30*I/J+15):GOTO 4000
3600 IF (I/J>=0.44 AND I/J<0.8) THEN TYU=90-(42*I/J+5.5):GOTO 4000
3700 IF I/J<0.44 THEN TYU=90-(55*I/J):GOTO 4000
4000 '
4100 HAIJO=42/SQR(I*I+J*J)
4200 IF I=1 AND J=0 THEN HAIJO=45
4300 IF I=1 AND J=1 THEN HAIJO=30
4400 ARCRYAK(I,J,1)=TYU-HAIJO
4500 ARCRYAK(I,J,2)=TYU+HAIJO
4800 NEXT J
4900 NEXT I
5000 '
5002 CONT%=0
5100 FOR I=1 TO 8:FOR J=0 TO 8:FOR K=1 TO 2
5200 CONT%=CONT%+1
5300 ARCRYAKL(CONT%)=ARCRYAK(I,J,K)
5400 ARCRYAKN$(CONT%)=ARCNA$(I,J,K)
5500 NEXT K:NEXT J:NEXT I
5600 '
5700 FOR I=1 TO 8
5800 FOR J=0 TO 8
5820 TYU=RADOODO*ATN(J/I)
5900 HAIJO=RADOODO*ATN(HANKEI/SQR(I*I+J*J-0.5))
6000 ARCGEN(I,J,1)=TYU-HAIJO
6100 ARCGEN(I,J,2)=TYU+HAIJO
6200 NEXT J
6300 NEXT I
6400 '
7100 CONT%=0
7200 FOR I=1 TO 8:FOR J=0 TO 8:FOR K=1 TO 2
7300 CONT%=CONT%+1
7400 ARCGENL(CONT%)=ARCGEN(I,J,K)
7500 ARCGENN$(CONT%)=ARCNA$(I,J,K+2)
7600 NEXT K:NEXT J:NEXT I
7700 CONT%=0
7900 '
8000 FOR I=1 TO 143
8100 FOR J=I+1 TO 144
8200 IF ARCRYAKL(I)>ARCRYAKL(J) THEN SWAP ARCRYAKL(I),ARCRYAKL(J):SWAP ARCRYAKN$(I),ARCRYAKN$(J)
8400 IF ARCGENL(I)>ARCGENL(J) THEN SWAP ARCGENL(I),ARCGENL(J):SWAP ARCGENN$(I),ARCGENN$(J)
8600 NEXT J
8700 NEXT I
9000 '
9100 FOR I=1 TO 72
9200 PRINT #1, USING "##;& &;####.######;& &;####.#####";I,ARCRYAKN$(I),ARCRYAKL(I),ARCGENN$(I),ARCGENL(I)
9300 NEXT I
9320 CLOSE #1
9400 END
実行させると次のように答えが出るので、問題点
をタイピングして、抽出している。
なお以下は1行毎に、”順位、升目、限界角種類、方位角計算結果、
升目、限界角種類、方位角計算結果”を示している。
1; 1 0 計下 ; -45.000000; 1 0 厳下 ; -45.00000
2; 2 0 計下 ; -21.000000; 2 0 厳下 ; -20.70481
3; 3 0 計下 ; -14.000000; 3 0 厳下 ; -13.63302
4; 4 0 計下 ; -10.500000; 4 0 厳下 ; -10.18207
5; 5 0 計下 ; -8.400000; 5 0 厳下 ; -8.13010
6; 6 0 計下 ; -7.000000; 6 0 厳下 ; -6.76810
7; 7 0 計下 ; -6.000000; 7 0 厳下 ; -5.79764
8; 8 0 計下 ; -5.250000; 8 0 厳下 ; -5.07090
9; 8 1 計下 ; 1.665541; 8 1 厳下 ; 2.09338
10; 7 1 計下 ; 1.917446; 7 1 厳下 ; 2.39093
11; 6 1 計下 ; 2.261909; 6 1 厳下 ; 2.78673
12; 5 1 計下 ; 2.763122; 5 1 厳下 ; 3.33875
13; 4 1 計下 ; 3.563504; 4 1 厳下 ; 4.16128
14; 3 1 計下 ; 5.051767; 8 0 厳上 ; 5.07090
15; 8 0 計上 ; 5.250000; 3 1 厳下 ; 5.51398
16; 7 0 計上 ; 6.000000; 7 0 厳上 ; 5.79764
17; 6 0 計上 ; 7.000000; 6 0 厳上 ; 6.76810
18; 2 1 計下 ; 7.717029; 5 0 厳上 ; 8.13010←要注意
19; 5 0 計上 ; 8.400000; 2 1 厳下 ; 8.13010←
20; 8 2 計下 ; 8.656752; 8 2 厳下 ; 9.11713
21; 7 2 計下 ; 9.945142; 4 0 厳上 ; 10.18207←問題なし
22; 4 0 計上 ; 10.500000; 7 2 厳下 ; 10.37155←
23; 6 2 計下 ; 11.692550; 6 2 厳下 ; 12.01566
24; 8 1 計上 ; 12.084459; 8 1 厳上 ; 12.15665
25; 7 1 計上 ; 13.796840; 3 0 厳上 ; 13.63302←議論済
26; 3 0 計上 ; 14.000000; 7 1 厳上 ; 13.86927←
27; 5 2 計下 ; 14.200796; 5 2 厳下 ; 14.25632
28; 1 1 計下 ; 15.000000; 1 1 厳下 ; 15.00000
29; 8 3 計下 ; 15.709272; 8 3 厳下 ; 15.80878
30; 6 1 計上 ; 16.071424; 6 1 厳上 ; 16.13791
31; 4 2 計下 ; 17.108514; 4 2 厳下 ; 17.46762
32; 7 3 計下 ; 18.056558; 7 3 厳下 ; 17.87114
33; 8 2 計上 ; 18.843248; 8 2 厳上 ; 18.95536
34; 5 1 計上 ; 19.236878; 5 1 厳上 ; 19.28112
35; 6 3 計下 ; 20.239010; 6 3 厳下 ; 20.51431
36; 2 0 計上 ; 21.000000; 2 0 厳上 ; 20.70481
37; 7 2 計上 ; 21.483429; 7 2 厳上 ; 21.51924
38; 8 4 計下 ; 21.804257; 8 4 厳下 ; 22.03069
39; 3 2 計下 ; 21.851296; 3 2 厳下 ; 22.38014
40; 5 3 計下 ; 23.497059; 4 1 厳上 ; 23.91120←問題なし
41; 4 1 計上 ; 23.936496; 5 3 厳下 ; 23.99848←
42; 7 4 計下 ; 24.290541; 7 4 厳下 ; 24.71324
43; 6 2 計上 ; 24.974116; 6 2 厳上 ; 24.85423
44; 8 3 計上 ; 25.540728; 8 3 厳上 ; 25.30331
45; 8 5 計下 ; 27.298009; 8 5 厳下 ; 27.70685
46; 6 4 計下 ; 27.675648; 6 4 厳下 ; 28.06271
47; 4 3 計下 ; 28.600000; 7 3 厳上 ; 28.52604←問題なし
48; 7 3 計上 ; 29.086299; 4 3 厳下 ; 28.73980←
49; 5 2 計上 ; 29.799204; 5 2 厳上 ; 29.34650
50; 2 2 計下 ; 30.150758; 2 2 厳下 ; 30.52249
51; 7 5 計下 ; 30.617599; 7 5 厳下 ; 30.82267
52; 8 4 計上 ; 31.195743; 8 4 厳上 ; 31.09941
53; 3 1 計上 ; 31.614900; 3 1 厳上 ; 31.35592
54; 5 4 計下 ; 32.440702; 5 4 厳下 ; 32.31962
55; 6 3 計上 ; 32.760990; 6 3 厳上 ; 32.61580
56; 8 6 計下 ; 32.800000; 8 6 厳下 ; 32.81509
57; 6 5 計下 ; 34.622451; 6 5 厳下 ; 34.61114
58; 7 4 計上 ; 34.709459; 7 4 厳上 ; 34.77652
59; 3 3 計下 ; 35.100505; 3 3 厳下 ; 35.40593
60; 4 2 計上 ; 35.891486; 4 2 厳上 ; 35.66249
61; 7 6 計下 ; 36.158746; 7 6 厳下 ; 36.20259
62; 8 5 計上 ; 36.201991; 8 5 厳上 ; 36.30391
63; 8 7 計下 ; 37.298972; 8 7 厳下 ; 37.37185
64; 4 4 計下 ; 37.575379; 4 4 厳下 ; 37.81924
65; 5 3 計上 ; 37.902941; 5 3 厳上 ; 37.92903
66; 5 5 計下 ; 39.060303; 5 5 厳下 ; 39.26083
67; 6 4 計上 ; 39.324352; 6 4 厳上 ; 39.31742
68; 6 6 計下 ; 40.050253; 6 6 厳下 ; 40.21981
69; 7 5 計上 ; 40.382401; 7 5 厳上 ; 40.25268
70; 7 7 計下 ; 40.757359; 7 7 厳下 ; 40.90396
71; 8 6 計上 ; 41.200000; 8 6 厳上 ; 40.92470
72; 8 8 計下 ; 41.287689; 8 8 厳下 ; 41.41668
上記の結果リストから判るように、9×9升目
盤では所詮、チェックが必要な方位角計算は、
事実上この、72通りしか無いのである。
そして、右隅のコメントのように
暗算の為の略計算では5箇所、厳密計算
との間に、違いが生じている。
ただし、途中駒がターゲット駒を隠すというカテ
ゴリーの間違いは冒頭で紹介した「7の1の上限
よりも3の0の上限の方が小さい」という1箇所
だけである。
残りの4箇所は、厳密計算では角道状の穴から、
向こうの駒を突きぬいて取れるのに、略算すると、
穴が無くなるという「角道類似型間違い」だけ
である。排除円の半径を、遠方で過大に見ている
のが、差異が生じる主原因だと私は解釈する。
そのうち以下説明するケースを除く3つは、私
には将棋盤を見ても、にわかにはピンと来ない
ケースである。例えば上記のリストで40と41
の逆転については「略算だと、そういうものか」
と私なら諦める例か?
これらは、間違っていても略算結果が正しいとし
て非合法にしてしまって、問題無いのではないか
と疑われるという意味である。
残りの一つで、上記で要注意とした一番上のケー
スというのは、
初期位置の5八位置に、超奔王が最初居るとして、
超奔王先の歩兵は突き捨てる位置5四に居て、盤
面には、自陣の金将前と超奔王前の3歩だけ有っ
て残りの15個の歩兵は無いとしたときに、以前
述べたように、超奔王位置から、相手陣両金将位
置の駒はその場合にも直射するのだが、仮に味方
の玉将が、別の位置に移動済みで、一歩超奔王自
身が後退して
▲5九超奔王としても、味方の金将前3段目両歩
兵と、味方の5四位値の、突き捨て歩兵の2枚組
「途中の駒」の間に、無限小の大きさの角道型穴
が空いていて、相手陣の両金将位置駒を、その無
限小の大きさの穴で突き刺せる
のではいかと、例示されるようなケースである。
厳密計算結果は、私は大学受験のときチェック
漏れしたが、2円の共通外接線の傾きが特定の場
合のケースであるらしく、5九の奔王位置から、
共通外接線光路で、相手陣金将位置の駒が無限小
の角度で覗いているらしい。
このケースは、超奔王を1歩後退しても、相手
金将位置駒が取れるというルールが「小気味良い」
感じなので、厳密計算と無限小の次数解析(この
場合も同次の無限小だとみられる)で、いっけん
厳密計算を採用したくもなる、例外
のようにも感じる。
特に、相手が幾何学が強い棋士なら、突っ込み
が入るかもしれない。継続して、議論すべきかと
思う。
上記のNo.18と19の、2の1と5の0で、
無限小の穴を作る例だけ、そのうち円の共通接線
の幾何学で、チェックしてみようと私は考えた。
(2023/10/28)
超奔王、略暗算で先歩二歩上げても相手金取れず(長さん)
既に述べたように、1升目先の「途中の駒」
が超奔王に対して45°(-δ;δ→0)の
排除視半径を持つ、アナログで走れる超奔王を
含む日本将棋盤使用、持駒46枚制将棋で、
超奔王ルールの合否判断略算法を検討してきた。
1の1が視半径30°、2の0/0の2以遠
を42°の逆数と近似、更に本ブログ独自の、
正接から方位角を計算する方法を略算法として
提示した。厳密な計算も電卓と数表から容易な
為、略算の誤差によって問題が発生する箇所の
有無をチェックした。
非合法なのに合法としてしまうケースは、
多分だが余り無いようだった。
今回は、それでも
略算で非合法になるが、実際には合法で、
計算がぽんやりしすぎている、以下のケース
について、現状と対策を考察
した。
問題となった例は、初期配列5八の位置に
超奔王が居るとして、超奔王先の歩兵しか、
歩兵が双方に全く無い、17枚歩兵が消えた
仮想のケースで、相手金位置の相手駒が、
略算だと、2歩上げた超奔王先の歩兵で、遮蔽
されているように、間違って計算してしまう
という問題である。
ここで問題にしているケースを計算すると、
ざっと、次のようになる。
暗算だと。
7の1の駒の距離は、√50升。方位角が、
55×1/7で7.857°、駒の視半径は
4.2×√2≒5.94=(5.88+0.06)
で、カッコの中を頭の中で暗算である。
3の0の駒の距離は3。方位角が0°。
駒の視半径は14°。
よって、方位角差は、7.857°
14-7.857=6.143°より、
6.143>5.94°で、合法である。
そこで次に。
数表を使うと7の1の駒の距離は、√50升。
方位角が8.12°で、視半径は、ぴたり
arcsin(0.1)であり約5.75°。
3の0の駒の距離は、3。方位角が、0°
駒の視半径は数表によりarcSin(√2/6)
で、約13.63°。
方位角差が8.12°で、排除円の許容は
13.63°-8.12°=5.51°で
5.51°<5.75°で、非合法となり
このケースは、逆転する。
つまり、相手陣の金将位置に居る駒は、
手前の超奔王の居る5筋で歩兵を、天王山の
▲5五歩まで上げると見えるはずなのに、略算
では、完全に隠れる事になるのである。
それに対し、厳密計算だと「一部見える」
という、真逆の結果となり、実際には盤の交点
を観察すると、
良く見ると、合法のように見える
という場合になっている。
そこで、このようなケースの対策を考察す
ると、このケースは、一歩超奔王先の歩兵を
上げた状態で、相手1段目が超奔王から、
全部遮蔽される状態から、銀と金と玉の3枚
が遮蔽されるに変わり、2歩上げると正確に
計算すると、実際には、玉だけ遮蔽されるの
だが、略算誤差で玉と金が遮蔽されたままに
なり、突き捨てる位置(~▲5四歩)で、玉
だけ隠すというルールになってしまうので、
良く考えると、ルールの「調子が取れている」
ので、
厳密性は無視して、略算を真とするのも、悪く
は無い、特別のケースなのではないか
と本ブログの管理人は私見する。
問題はかなり大きいが、ぎりぎりで我慢する
といったケース、という訳ではなかろうか。
ちなみに、誤差の原因は、排除円の半径の
見積もり誤差と、方位角の略計算誤差が、
このケースは、だいたい拮抗するという問題
を解決し難いという点で、
「最悪のパターン」である。
しかし、こんな問題が、ルールを決定しよ
うとした当初、有るとは私には想定もし無かっ
た。まだ、とりあえずビックリしたという私
は、レベルに在る。(2023/10/27)
が超奔王に対して45°(-δ;δ→0)の
排除視半径を持つ、アナログで走れる超奔王を
含む日本将棋盤使用、持駒46枚制将棋で、
超奔王ルールの合否判断略算法を検討してきた。
1の1が視半径30°、2の0/0の2以遠
を42°の逆数と近似、更に本ブログ独自の、
正接から方位角を計算する方法を略算法として
提示した。厳密な計算も電卓と数表から容易な
為、略算の誤差によって問題が発生する箇所の
有無をチェックした。
非合法なのに合法としてしまうケースは、
多分だが余り無いようだった。
今回は、それでも
略算で非合法になるが、実際には合法で、
計算がぽんやりしすぎている、以下のケース
について、現状と対策を考察
した。
問題となった例は、初期配列5八の位置に
超奔王が居るとして、超奔王先の歩兵しか、
歩兵が双方に全く無い、17枚歩兵が消えた
仮想のケースで、相手金位置の相手駒が、
略算だと、2歩上げた超奔王先の歩兵で、遮蔽
されているように、間違って計算してしまう
という問題である。
ここで問題にしているケースを計算すると、
ざっと、次のようになる。
暗算だと。
7の1の駒の距離は、√50升。方位角が、
55×1/7で7.857°、駒の視半径は
4.2×√2≒5.94=(5.88+0.06)
で、カッコの中を頭の中で暗算である。
3の0の駒の距離は3。方位角が0°。
駒の視半径は14°。
よって、方位角差は、7.857°
14-7.857=6.143°より、
6.143>5.94°で、合法である。
そこで次に。
数表を使うと7の1の駒の距離は、√50升。
方位角が8.12°で、視半径は、ぴたり
arcsin(0.1)であり約5.75°。
3の0の駒の距離は、3。方位角が、0°
駒の視半径は数表によりarcSin(√2/6)
で、約13.63°。
方位角差が8.12°で、排除円の許容は
13.63°-8.12°=5.51°で
5.51°<5.75°で、非合法となり
このケースは、逆転する。
つまり、相手陣の金将位置に居る駒は、
手前の超奔王の居る5筋で歩兵を、天王山の
▲5五歩まで上げると見えるはずなのに、略算
では、完全に隠れる事になるのである。
それに対し、厳密計算だと「一部見える」
という、真逆の結果となり、実際には盤の交点
を観察すると、
良く見ると、合法のように見える
という場合になっている。
そこで、このようなケースの対策を考察す
ると、このケースは、一歩超奔王先の歩兵を
上げた状態で、相手1段目が超奔王から、
全部遮蔽される状態から、銀と金と玉の3枚
が遮蔽されるに変わり、2歩上げると正確に
計算すると、実際には、玉だけ遮蔽されるの
だが、略算誤差で玉と金が遮蔽されたままに
なり、突き捨てる位置(~▲5四歩)で、玉
だけ隠すというルールになってしまうので、
良く考えると、ルールの「調子が取れている」
ので、
厳密性は無視して、略算を真とするのも、悪く
は無い、特別のケースなのではないか
と本ブログの管理人は私見する。
問題はかなり大きいが、ぎりぎりで我慢する
といったケース、という訳ではなかろうか。
ちなみに、誤差の原因は、排除円の半径の
見積もり誤差と、方位角の略計算誤差が、
このケースは、だいたい拮抗するという問題
を解決し難いという点で、
「最悪のパターン」である。
しかし、こんな問題が、ルールを決定しよ
うとした当初、有るとは私には想定もし無かっ
た。まだ、とりあえずビックリしたという私
は、レベルに在る。(2023/10/27)
本ブログ方式方位角略算式の精度の確認(長さん)
今回は以前に引き続いて、本ブログ版奔将棋
の超奔王が右香車位置に居るとして、そこか
ら飛車先歩兵を1歩上げたときに、相手玉将
に直射し無くなっているのかという、0の0
位置駒から見て、3の1位置駒が8の4駒を、
1升目45°(-δ)排除円ルールで、辛くも
隠していると出来るのかどうかを、確認する
話題である。今回は、一松信著「初等関数の
数値計算」のarcTanの近似式を改善し、
方位角は正弦が0.4285まで55×正弦、
正弦がそれ以上0.8未満まで42×正弦+5.5、
正弦が0.8以上1まで30×正弦+15
の本ブログ版新方式を採用した。なお排除円
は、1の0/0の1で45°(-δ;δ→0)、
1の1で30°、それより遠方で隣42°の
逆比例近似で、まずはチェックした。その他、
関連するテストの例について、多少言及する。
なお遠方で比例定数が本当は、180/√2π=
40.51423になるのを、暗算の容易性か
ら42にしたやり方は、誤差をほどよく吸収し、
超奔王ルールで、禁手を合法手だと計算違い
して指さないようにするという、「あわて者型
間違」は、絶対に防止するのに、良いやり方の
ように見えたので採用したのであった。
結果を以下に述べる。
新しい方位角近似計算だと、次のようになる。
3の1の駒の視半径は14-0.72で、
約13.28°(14から差が渚の「ナギ72」)。
方位角は55/3で18.3°距離√10。
これは、正弦0.4285まで、近似式が同じ
なので、変化は無い。
次に8の4の駒の距離は√80升。方位角が、
こんどは42×0.5+5.5で26.5°に
なる。以前のやり方だと、一松信「初等関数の
数値計算」で同1/2以上の近似式:
40×0.5+7で27.0°に、したので
あった。
方位角差8.2°で13.28の差5.08、
13.28/5.08・・で約2.614倍以
遠で非合法。√(80/10)は2.828倍
だから、略計算でも今度は、逆比例の比例定数
を大きくしている効果が効き、以前言及した通
り、略算でも非合法手になった。
より正しい数表計算では3の1の駒の視半経
は12.93°。方位角は18.43°。距離
√10。
8の4の駒の方位角が26.57°。
方位角差は8.14°と同程度であり、
12.93・・/4.79・・=2.70倍
以遠で非合法と以前に説明した。
次に、今度は相手玉将の8の4位置に、ター
ゲットでは無くて、邪魔な一枚目の隠す駒があ
り、飛車先1歩上げ歩兵では無くてそれと斜め
に接する2の2の位置の、味方銀先の歩兵が、
第二の隠す駒になっていて、8の5の位置の、
相手陣の右金が初期位置に、超奔王で取りたい
駒があるという、2つの「手前の途中の駒」に、
隙間が存在するかもしれないので、そこを突き
抜けて、相手陣右金将位置駒を取れ無いのかと
いう問題について考えてみる。
先の問題とは、升目の接点の組み合わせが同じ
の、「類似問題」である。
先に述べたように、
8の4の駒の距離は、√80升。方位角が、
42×0.5+5.5で26.5°、駒の視半
径は18.782971(岩魚は肉無い)/4
である。(この時点で暗算し無くてもよいが、
4.6957°位。)
2の2の駒の距離は、√8升。方位角が、
正弦1で30×1+15で45°。ただし自明。
駒の視半径は15×0.99で、14.85°
とするはずであった。√2が1.4では無くて、
1.414に近いから1-0.01掛けである。
よって、方位角差は、18.5°。
これより小さいと「穴」が開く排除円の合計は、
14.85×(1+1/√10)=19.54・・
度。この計算は14の2乗/10に近く、だいたい
19.6になるのは見えているので、穴は見え
ないはずである。
そこで次に。
数表を使うと8の4の駒の距離は、√80升。
方位角が26.57°で、視半径は4.53°
2の2の駒の距離は、√8升。方位角が、
45°。駒の視半径は数表により14.48°。
方位角差が18.43°で、排除円の合計は
14.48+4.53°=19.01°
排除円を少し大きく見積もる為、このような
ケースは、逆転の危険が有るのだが。
このケースもまだ大丈夫なようである。ただし、
一松信「初等関数の数値計算」通りに、
馬鹿正直に正弦0.5で27°、1で47°に
でもしてしまうと、最初の例といっしょで、
方位角差20°となり、非合法が合法になると
いう事
である。
以上の事から方位角の一松信近似で、やはり
正弦0.5と同1の計算の精度が。跳びぬけて
悪いという、比較的単純な弱点が致命的
なのであり。9升目将棋計算用では、なんらか
の方法で、方位角略算の、その問題を解決する
事が、キモである事は確かかと思えるように、
私にはなって来た。(2023/10/26)
の超奔王が右香車位置に居るとして、そこか
ら飛車先歩兵を1歩上げたときに、相手玉将
に直射し無くなっているのかという、0の0
位置駒から見て、3の1位置駒が8の4駒を、
1升目45°(-δ)排除円ルールで、辛くも
隠していると出来るのかどうかを、確認する
話題である。今回は、一松信著「初等関数の
数値計算」のarcTanの近似式を改善し、
方位角は正弦が0.4285まで55×正弦、
正弦がそれ以上0.8未満まで42×正弦+5.5、
正弦が0.8以上1まで30×正弦+15
の本ブログ版新方式を採用した。なお排除円
は、1の0/0の1で45°(-δ;δ→0)、
1の1で30°、それより遠方で隣42°の
逆比例近似で、まずはチェックした。その他、
関連するテストの例について、多少言及する。
なお遠方で比例定数が本当は、180/√2π=
40.51423になるのを、暗算の容易性か
ら42にしたやり方は、誤差をほどよく吸収し、
超奔王ルールで、禁手を合法手だと計算違い
して指さないようにするという、「あわて者型
間違」は、絶対に防止するのに、良いやり方の
ように見えたので採用したのであった。
結果を以下に述べる。
新しい方位角近似計算だと、次のようになる。
3の1の駒の視半径は14-0.72で、
約13.28°(14から差が渚の「ナギ72」)。
方位角は55/3で18.3°距離√10。
これは、正弦0.4285まで、近似式が同じ
なので、変化は無い。
次に8の4の駒の距離は√80升。方位角が、
こんどは42×0.5+5.5で26.5°に
なる。以前のやり方だと、一松信「初等関数の
数値計算」で同1/2以上の近似式:
40×0.5+7で27.0°に、したので
あった。
方位角差8.2°で13.28の差5.08、
13.28/5.08・・で約2.614倍以
遠で非合法。√(80/10)は2.828倍
だから、略計算でも今度は、逆比例の比例定数
を大きくしている効果が効き、以前言及した通
り、略算でも非合法手になった。
より正しい数表計算では3の1の駒の視半経
は12.93°。方位角は18.43°。距離
√10。
8の4の駒の方位角が26.57°。
方位角差は8.14°と同程度であり、
12.93・・/4.79・・=2.70倍
以遠で非合法と以前に説明した。
次に、今度は相手玉将の8の4位置に、ター
ゲットでは無くて、邪魔な一枚目の隠す駒があ
り、飛車先1歩上げ歩兵では無くてそれと斜め
に接する2の2の位置の、味方銀先の歩兵が、
第二の隠す駒になっていて、8の5の位置の、
相手陣の右金が初期位置に、超奔王で取りたい
駒があるという、2つの「手前の途中の駒」に、
隙間が存在するかもしれないので、そこを突き
抜けて、相手陣右金将位置駒を取れ無いのかと
いう問題について考えてみる。
先の問題とは、升目の接点の組み合わせが同じ
の、「類似問題」である。
先に述べたように、
8の4の駒の距離は、√80升。方位角が、
42×0.5+5.5で26.5°、駒の視半
径は18.782971(岩魚は肉無い)/4
である。(この時点で暗算し無くてもよいが、
4.6957°位。)
2の2の駒の距離は、√8升。方位角が、
正弦1で30×1+15で45°。ただし自明。
駒の視半径は15×0.99で、14.85°
とするはずであった。√2が1.4では無くて、
1.414に近いから1-0.01掛けである。
よって、方位角差は、18.5°。
これより小さいと「穴」が開く排除円の合計は、
14.85×(1+1/√10)=19.54・・
度。この計算は14の2乗/10に近く、だいたい
19.6になるのは見えているので、穴は見え
ないはずである。
そこで次に。
数表を使うと8の4の駒の距離は、√80升。
方位角が26.57°で、視半径は4.53°
2の2の駒の距離は、√8升。方位角が、
45°。駒の視半径は数表により14.48°。
方位角差が18.43°で、排除円の合計は
14.48+4.53°=19.01°
排除円を少し大きく見積もる為、このような
ケースは、逆転の危険が有るのだが。
このケースもまだ大丈夫なようである。ただし、
一松信「初等関数の数値計算」通りに、
馬鹿正直に正弦0.5で27°、1で47°に
でもしてしまうと、最初の例といっしょで、
方位角差20°となり、非合法が合法になると
いう事
である。
以上の事から方位角の一松信近似で、やはり
正弦0.5と同1の計算の精度が。跳びぬけて
悪いという、比較的単純な弱点が致命的
なのであり。9升目将棋計算用では、なんらか
の方法で、方位角略算の、その問題を解決する
事が、キモである事は確かかと思えるように、
私にはなって来た。(2023/10/26)
略Arctan近似計算のやり方の改善(長さん)
現代では、エクセル関数や言語の関数にarcTan
は実装されていて、近似式で略算することは滅多に
無いのであろうが。計算機が今ほど普及し無かった
前世紀には、教育出版、新しい応用の数学8
「初等関数の数値計算」、一松信著に、arcTan
の、折れ線近似の式が載っていたりもした。
関数電卓等は持込不可だとして、暗算で物体の運動
による直角座標の変化から、極座標の方位角を求める
際に、便利だと私的に感じている。が、具体的に前記
成書の方位角計算近似式は、既に紹介している奔将棋
の、自由にどんなアナログ角度に走れる、(仮称)
「超奔王」駒の走る升目数を知って、その方向の方位
角を計算するには、精度が不足である事を以前、本ブ
ログで示してきた。今回は、前記成書の近似式を、
近似する折れ線の数を2本から3本に増やす事により、
将棋で遊ぶレベルでは、必要な精度を出してみよう
とする試みの紹介である。
3/7(0の0升目を起点として3の7か、7の3
位置に動く)が正弦値で、それを小数に直すと
0.4285・・倍程度までを、従来の一松信式の、
55×正弦とし、
0.5ではなくて0.4285・・程度を超え0.8
未満を42×正弦+5.5、それ以上で1.0倍まで、
30×正弦+15と、3つに分ける、
やり方を、本ブログでは独自に考えた。
簡単に経過を記す。
折れ線近似を踏襲する限り、
前記成書の精度が、飛びぬけて上がるやり方は無い
ようである。そこで、
式が2つでは無くて、3つ程度までなら我慢も出来る
だろうと、私は考えた。特に、
40×分数+7と42×分数+5.5は、煩雑性に
差が感じられないので、0.5から0.4285・・
へ、使用する変数域の下限をシフトさせておいて、
40×正弦+7を42×正弦+5.5に変えた。
42は代入する数値が分数になるとき使いやすいし、
5.5は0.4285・・まで使った倍数の1/10
なので、元の式と比較しても、
より、覚えやすかろう
と私は考えた。そうすると、正弦が0.8以上になる
と、一松信式よりも精度が悪くなる。ので、別に
変数域が0.8以上の場合について、
30×正弦+15を持ってきた。
30は40の10違いで、元の0.5以上の式と似て
いて覚えやすいし、15も覚えやすいし、正弦が1の
ときに、30+15で45°だからと、屁理屈をこね
れば、記憶は容易だろう。
こうして近似で当てはめる折れ線を増やすと、以下
の誤差計算グラフのように左から右の挙動に変化して、
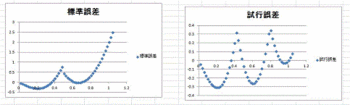
紹介した成書のときよりも、極端に値が異なる場合
が無くなる。
特に、0.5が27~27.5°から26.5°に
変わるのが大きいし、1が47°からぴたりと45°
になる。
3の1で8の4駒が隠れるかという問題での合否の
逆転問題は、明らかにこの変更で解決するし、そもそ
も0.5が26.57°、1が45°(こっちは当た
り前だが)が、”暗記”という事も無くなるので、
覚える式が増加する手間を効果が上回る事は、恐らく
確かだろうと、私は考えている。(2023/10/25)
は実装されていて、近似式で略算することは滅多に
無いのであろうが。計算機が今ほど普及し無かった
前世紀には、教育出版、新しい応用の数学8
「初等関数の数値計算」、一松信著に、arcTan
の、折れ線近似の式が載っていたりもした。
関数電卓等は持込不可だとして、暗算で物体の運動
による直角座標の変化から、極座標の方位角を求める
際に、便利だと私的に感じている。が、具体的に前記
成書の方位角計算近似式は、既に紹介している奔将棋
の、自由にどんなアナログ角度に走れる、(仮称)
「超奔王」駒の走る升目数を知って、その方向の方位
角を計算するには、精度が不足である事を以前、本ブ
ログで示してきた。今回は、前記成書の近似式を、
近似する折れ線の数を2本から3本に増やす事により、
将棋で遊ぶレベルでは、必要な精度を出してみよう
とする試みの紹介である。
3/7(0の0升目を起点として3の7か、7の3
位置に動く)が正弦値で、それを小数に直すと
0.4285・・倍程度までを、従来の一松信式の、
55×正弦とし、
0.5ではなくて0.4285・・程度を超え0.8
未満を42×正弦+5.5、それ以上で1.0倍まで、
30×正弦+15と、3つに分ける、
やり方を、本ブログでは独自に考えた。
簡単に経過を記す。
折れ線近似を踏襲する限り、
前記成書の精度が、飛びぬけて上がるやり方は無い
ようである。そこで、
式が2つでは無くて、3つ程度までなら我慢も出来る
だろうと、私は考えた。特に、
40×分数+7と42×分数+5.5は、煩雑性に
差が感じられないので、0.5から0.4285・・
へ、使用する変数域の下限をシフトさせておいて、
40×正弦+7を42×正弦+5.5に変えた。
42は代入する数値が分数になるとき使いやすいし、
5.5は0.4285・・まで使った倍数の1/10
なので、元の式と比較しても、
より、覚えやすかろう
と私は考えた。そうすると、正弦が0.8以上になる
と、一松信式よりも精度が悪くなる。ので、別に
変数域が0.8以上の場合について、
30×正弦+15を持ってきた。
30は40の10違いで、元の0.5以上の式と似て
いて覚えやすいし、15も覚えやすいし、正弦が1の
ときに、30+15で45°だからと、屁理屈をこね
れば、記憶は容易だろう。
こうして近似で当てはめる折れ線を増やすと、以下
の誤差計算グラフのように左から右の挙動に変化して、

紹介した成書のときよりも、極端に値が異なる場合
が無くなる。
特に、0.5が27~27.5°から26.5°に
変わるのが大きいし、1が47°からぴたりと45°
になる。
3の1で8の4駒が隠れるかという問題での合否の
逆転問題は、明らかにこの変更で解決するし、そもそ
も0.5が26.57°、1が45°(こっちは当た
り前だが)が、”暗記”という事も無くなるので、
覚える式が増加する手間を効果が上回る事は、恐らく
確かだろうと、私は考えている。(2023/10/25)
暗算1升離45°排除円超奔王ルール将棋にトラブル(長さん)
今回は日本将棋状の9升目持駒46枚制将棋に、
気体の分子運動論状の駒、超奔王を1種類だけ
入れた、新作将棋の話題の続きである。
今までの所で、1升目離れた所の、近くに
ある「途中の駒」が超奔王の直進に対して、
無限に小さい角道は作れる視半径45°の排除
領域を持つとして、超奔王の「走りルール」を
定義すれば、一松信方式の方位角の近似計算に
よる暗算と、0の1/1の0から5の5までの
升目についての、排除円半径を0の1/1の0
は45°(-δ)、1の1は30°ちょうど、
その先は42/升目数近似で、必要に応じて、
暗記数値で”遮蔽駒があり、超奔王を動かす
際の『途中の駒』になるのかどうかで着手の合
否判定をする”という判定方法として、それで
良いのではないかと、述べてきた。
特に、厳密に計算すると0の2/2の0の場
合、arcCosec(4/√2)=
arcCosec(1/0.3535533)=
arcSin(0.3535533)≒
20.7°<21°(=42°/2)になるの
で、遠方で比例定数が本当は、180/√2π=
40.51423になるのを、暗算の容易性か
ら42にしたやり方は、誤差をほどよく吸収し、
超奔王ルールで、禁手を合法手だと計算違いし
て指さないようにするという、「あわて者型間
違」は、絶対に防止するのにも、いっけん良い
やり方のように、以前には見えたのであった。
ところが、以下のようなケース、暗算による
”『途中の駒』であるかどうかの近似計算”時、
今まで述べたやり方だと、『途中の駒』なのに、
間はすり抜けられると計算してしまい、非合法
手を指してしまう問題が
1例だけあるのを、本ブログの管理人は見出し
た。そしてその回避策は、2の1/1の2向う
桂馬跳びパターンの方位角を、一松信式近似計
算結果を使わずに、26.57°か26.6°
だと”暗記する”しか無さそうだ。
単刀直入に、問題の有るケースを述べると、
0の0の位置に有る超奔王が、3の1の位置に、
「途中の駒」が有るように見えるときに、
8の4の位置の駒は、本当は取れないようだ
という1ケースである。判りやすく言うと、「
右香車の位置に居る超奔王は、飛車先の歩兵が
初期位置に居ると、相手居玉の玉将を遮蔽する
のはもちろんだが、1歩上げてもまだ、超奔王
は直射せず、中段まで飛車先歩を上げないと、
玉将取りは、掛からない」等の例が挙げられる。
さて、この3の1の駒を通して8の4の駒が
取れるかどうかという問題について、対局中、
つぎのような略暗算が、これまでの議論で想定
されている。
3の1の駒の視半径は14-0.72で、
約13.28°(14から差が渚の「ナギ72」)。
方位角は55/3で18.3°距離√10。
8の4の駒の距離は√80升。方位角が、
一松信「初等関数の数値計算」でarcTan
で1/2以下の近似式で27.5°、同1/2
以上の近似式で27°。非合法の棄却検定だか
ら27°とする。
方位角差8.7°で13.28の差4.58、
13.28/4.58・・で約2.9倍以遠で
非合法。√(80/10)は2.828倍
だから、略計算では、
微かに縁が見えて、合法手のはずである。
なおここで13.28・・/4.58・・≒3
と誤魔化し略算しても、この論には影響無い。
ところが、三角関数表を見ながらより厳密に
計算すると、
3の1の駒の視半経は12.93°。
方位角は、18.43°。距離√10。
8の4の駒の方位角が26.57°。
よって、方位角差は8.14°と小さくなり、
12.93・・/4.79・・=2.70倍
以遠で非合法。よって√(80/10)は約
2.828倍だから、
完全に隠れて、非合法手
となってしまう。
厳密計算と、最初の略計算を比較すると、
8の4の駒の方位角の一松信略算式の1/2
のときの
26.57°からの0.5°ないし1°程度
の誤差、27.0°から27.5°との認識
の誤差が効いている
事が判る。つまり、arcTan計算で、
1/2のときだけ、一松信近似式を使わずに、
26.57と覚える以外どうにも仕方が無い
事が判る。
実は9升目盤のケースには、奇数が5より
大きいと1.5倍が8を超えるので、このよ
うな”反則負け”ケースの問題が、多分だが
起こら無い事が将棋盤をよく観察すると判る。
但し逆に、合法なのに略算して禁手と見てし
まうという「ぼんやり者型間違」のケースが、
少数起こる可能性が、有りそうだ。
”角道穴で、角道構成駒が全部取れるとい
うルールにしたという論を、前に本ブログで
は示したが。
向きが45°の場合以外は煩雑な為、スレ
スレは、全て非合法になるように、話を統一
するような、仕組みにした方が良いという事
かもしれない。なお、2:1/1:2升離を
26.57°とする事のほかに、一松信の方
位角略算では1:1のときに40+7で47°
になるが、これも暗記するまでも無く、45°
に、ルールではした方が良いようだ。
結論として特殊なケースとして、このよう
にした超奔王ルールの場合は、方位角角度と
その結果を暗記するしか、仕方が無いように、
残念ながら私には思えた。(2023/10/24)
気体の分子運動論状の駒、超奔王を1種類だけ
入れた、新作将棋の話題の続きである。
今までの所で、1升目離れた所の、近くに
ある「途中の駒」が超奔王の直進に対して、
無限に小さい角道は作れる視半径45°の排除
領域を持つとして、超奔王の「走りルール」を
定義すれば、一松信方式の方位角の近似計算に
よる暗算と、0の1/1の0から5の5までの
升目についての、排除円半径を0の1/1の0
は45°(-δ)、1の1は30°ちょうど、
その先は42/升目数近似で、必要に応じて、
暗記数値で”遮蔽駒があり、超奔王を動かす
際の『途中の駒』になるのかどうかで着手の合
否判定をする”という判定方法として、それで
良いのではないかと、述べてきた。
特に、厳密に計算すると0の2/2の0の場
合、arcCosec(4/√2)=
arcCosec(1/0.3535533)=
arcSin(0.3535533)≒
20.7°<21°(=42°/2)になるの
で、遠方で比例定数が本当は、180/√2π=
40.51423になるのを、暗算の容易性か
ら42にしたやり方は、誤差をほどよく吸収し、
超奔王ルールで、禁手を合法手だと計算違いし
て指さないようにするという、「あわて者型間
違」は、絶対に防止するのにも、いっけん良い
やり方のように、以前には見えたのであった。
ところが、以下のようなケース、暗算による
”『途中の駒』であるかどうかの近似計算”時、
今まで述べたやり方だと、『途中の駒』なのに、
間はすり抜けられると計算してしまい、非合法
手を指してしまう問題が
1例だけあるのを、本ブログの管理人は見出し
た。そしてその回避策は、2の1/1の2向う
桂馬跳びパターンの方位角を、一松信式近似計
算結果を使わずに、26.57°か26.6°
だと”暗記する”しか無さそうだ。
単刀直入に、問題の有るケースを述べると、
0の0の位置に有る超奔王が、3の1の位置に、
「途中の駒」が有るように見えるときに、
8の4の位置の駒は、本当は取れないようだ
という1ケースである。判りやすく言うと、「
右香車の位置に居る超奔王は、飛車先の歩兵が
初期位置に居ると、相手居玉の玉将を遮蔽する
のはもちろんだが、1歩上げてもまだ、超奔王
は直射せず、中段まで飛車先歩を上げないと、
玉将取りは、掛からない」等の例が挙げられる。
さて、この3の1の駒を通して8の4の駒が
取れるかどうかという問題について、対局中、
つぎのような略暗算が、これまでの議論で想定
されている。
3の1の駒の視半径は14-0.72で、
約13.28°(14から差が渚の「ナギ72」)。
方位角は55/3で18.3°距離√10。
8の4の駒の距離は√80升。方位角が、
一松信「初等関数の数値計算」でarcTan
で1/2以下の近似式で27.5°、同1/2
以上の近似式で27°。非合法の棄却検定だか
ら27°とする。
方位角差8.7°で13.28の差4.58、
13.28/4.58・・で約2.9倍以遠で
非合法。√(80/10)は2.828倍
だから、略計算では、
微かに縁が見えて、合法手のはずである。
なおここで13.28・・/4.58・・≒3
と誤魔化し略算しても、この論には影響無い。
ところが、三角関数表を見ながらより厳密に
計算すると、
3の1の駒の視半経は12.93°。
方位角は、18.43°。距離√10。
8の4の駒の方位角が26.57°。
よって、方位角差は8.14°と小さくなり、
12.93・・/4.79・・=2.70倍
以遠で非合法。よって√(80/10)は約
2.828倍だから、
完全に隠れて、非合法手
となってしまう。
厳密計算と、最初の略計算を比較すると、
8の4の駒の方位角の一松信略算式の1/2
のときの
26.57°からの0.5°ないし1°程度
の誤差、27.0°から27.5°との認識
の誤差が効いている
事が判る。つまり、arcTan計算で、
1/2のときだけ、一松信近似式を使わずに、
26.57と覚える以外どうにも仕方が無い
事が判る。
実は9升目盤のケースには、奇数が5より
大きいと1.5倍が8を超えるので、このよ
うな”反則負け”ケースの問題が、多分だが
起こら無い事が将棋盤をよく観察すると判る。
但し逆に、合法なのに略算して禁手と見てし
まうという「ぼんやり者型間違」のケースが、
少数起こる可能性が、有りそうだ。
”角道穴で、角道構成駒が全部取れるとい
うルールにしたという論を、前に本ブログで
は示したが。
向きが45°の場合以外は煩雑な為、スレ
スレは、全て非合法になるように、話を統一
するような、仕組みにした方が良いという事
かもしれない。なお、2:1/1:2升離を
26.57°とする事のほかに、一松信の方
位角略算では1:1のときに40+7で47°
になるが、これも暗記するまでも無く、45°
に、ルールではした方が良いようだ。
結論として特殊なケースとして、このよう
にした超奔王ルールの場合は、方位角角度と
その結果を暗記するしか、仕方が無いように、
残念ながら私には思えた。(2023/10/24)
なぜ大将棋の中段袖、猪・牛虎・竜で鼠兎要ら無い(長さん)
二中歴と普通唱導集を組み合わせると、大将棋
の中段には虎龍猪が有る事が判り、十二支の鼠・
兎は戦力不足とは言え、居無くて問題が無い、
何か理由が有りそうである。円形に満遍なく
「陣形」を作るのであれば、鶴翼の構えの如く
に十二支駒は、連続的に存在しないと、将棋駒
配列として不自然で、採用し難いように見える
のだが。少なくとも鎌倉時代の西暦1300年
頃、その不自然感が無かったように見える。
今回はこの歯抜け陣形の問題について、一考
する。
結論を先に書けば、
中世前期までの陣形は、大規模軍隊の戦闘が想
定されていても、縦長長方形陣程度の認識
であり、現代では著名な鶴翼の陣など、奇をて
らった陣形など、実戦で使われるとは思われて、
い無かったらしい。
そのような印象は、以下の成書から持てる。
「戦国の陣形」乃至政彦、講談社現代新書、
西暦2016年。
その40ページ付近に、白村江の戦の頃日本
で、25人×2隊体制の、弩等を武器として使
用した、長方形型の戦闘集団陣形が存在し、
保元の乱まで、その程度しか無かった(52
ページ)
と取れる記載がある。鎌倉時代まで簡単な陣形
しか、日本人は認識してい無かったようである。
中国からは、その間、本ブログ管理人には、
恐らく頭数の多い方形陣が輸入されたと、前記
成書には書かれているように認識される。50
人が1000人位に、なった(47ページ)ら
しい。察するに原野での中国の戦闘は、幅32
キロメートル、長さ3.2キロメートル程度に、
10メートル間隔で、100万人位の部隊を
編成し、弩・騎馬・兵が突進して相手を、
ブルトーザー式に押しつぶすというやり方が、
現実だったのであろう。戦闘が進んで、戦団が
横に広がったら、鶴翼の陣と、言った事は有っ
たのかもしれない。
日本の場合は、進路が狭いので、縦長になり、
かつ、規模は、鎌倉時代に多くて1万人程度を、
想像していただろうとみられる。鎌倉武家は、
軍勢であって、軍隊では無いから、国家間戦争
は、モンゴル帝国軍の来襲まで経験も無く、
将棋の陣形は当時は、想像上のものでしか無かっ
ただったとしか、言いようが無いのであろう。
方形の陣で攻める事を、牛駒の猛牛と虎駒の
猛虎で示して、鬼門を守る戦いを表現したと
して、牛軍と虎軍は、相手陣に縦長長方形陣で
攻め込むと、
相手陣は潰れて横に回り込んで来るので、横に
押さえに猪軍と龍軍が必要になるという、円で
は無くて、方形感覚だった
のでは無かろうか。
その為、斜め中間の鼠と兎は、敢えて絶対に、
必要とまで行かないという事では無かろうかと、
この成書の「中世前期の陣」を読んで、私は考
えるようになった。
前記成書にも、鶴翼陣といった戦形陣形は、
近世の作り物物語と取れる箇所が複数あるよう
に私には認識される。ようするに縦と横しか無
い陣形しか、国家間紛争時の軍勢には無い状態
を、鎌倉時代の武家が、国家の軍隊として想像
したので。大将棋の配置もそのような将棋配置
になったのではないかと、私は前記成書をざっ
と読みして考えるようになった。(2023/10/23)
の中段には虎龍猪が有る事が判り、十二支の鼠・
兎は戦力不足とは言え、居無くて問題が無い、
何か理由が有りそうである。円形に満遍なく
「陣形」を作るのであれば、鶴翼の構えの如く
に十二支駒は、連続的に存在しないと、将棋駒
配列として不自然で、採用し難いように見える
のだが。少なくとも鎌倉時代の西暦1300年
頃、その不自然感が無かったように見える。
今回はこの歯抜け陣形の問題について、一考
する。
結論を先に書けば、
中世前期までの陣形は、大規模軍隊の戦闘が想
定されていても、縦長長方形陣程度の認識
であり、現代では著名な鶴翼の陣など、奇をて
らった陣形など、実戦で使われるとは思われて、
い無かったらしい。
そのような印象は、以下の成書から持てる。
「戦国の陣形」乃至政彦、講談社現代新書、
西暦2016年。
その40ページ付近に、白村江の戦の頃日本
で、25人×2隊体制の、弩等を武器として使
用した、長方形型の戦闘集団陣形が存在し、
保元の乱まで、その程度しか無かった(52
ページ)
と取れる記載がある。鎌倉時代まで簡単な陣形
しか、日本人は認識してい無かったようである。
中国からは、その間、本ブログ管理人には、
恐らく頭数の多い方形陣が輸入されたと、前記
成書には書かれているように認識される。50
人が1000人位に、なった(47ページ)ら
しい。察するに原野での中国の戦闘は、幅32
キロメートル、長さ3.2キロメートル程度に、
10メートル間隔で、100万人位の部隊を
編成し、弩・騎馬・兵が突進して相手を、
ブルトーザー式に押しつぶすというやり方が、
現実だったのであろう。戦闘が進んで、戦団が
横に広がったら、鶴翼の陣と、言った事は有っ
たのかもしれない。
日本の場合は、進路が狭いので、縦長になり、
かつ、規模は、鎌倉時代に多くて1万人程度を、
想像していただろうとみられる。鎌倉武家は、
軍勢であって、軍隊では無いから、国家間戦争
は、モンゴル帝国軍の来襲まで経験も無く、
将棋の陣形は当時は、想像上のものでしか無かっ
ただったとしか、言いようが無いのであろう。
方形の陣で攻める事を、牛駒の猛牛と虎駒の
猛虎で示して、鬼門を守る戦いを表現したと
して、牛軍と虎軍は、相手陣に縦長長方形陣で
攻め込むと、
相手陣は潰れて横に回り込んで来るので、横に
押さえに猪軍と龍軍が必要になるという、円で
は無くて、方形感覚だった
のでは無かろうか。
その為、斜め中間の鼠と兎は、敢えて絶対に、
必要とまで行かないという事では無かろうかと、
この成書の「中世前期の陣」を読んで、私は考
えるようになった。
前記成書にも、鶴翼陣といった戦形陣形は、
近世の作り物物語と取れる箇所が複数あるよう
に私には認識される。ようするに縦と横しか無
い陣形しか、国家間紛争時の軍勢には無い状態
を、鎌倉時代の武家が、国家の軍隊として想像
したので。大将棋の配置もそのような将棋配置
になったのではないかと、私は前記成書をざっ
と読みして考えるようになった。(2023/10/23)
超奔王有り奔将棋44.5°ルールなおも煩雑(長さん)
気体の運動論を取り入れ、走り駒の走る方向
がアナログ角度で全てに亘る駒が一種類だけ
含まれる、日本将棋系の超奔王入り奔将棋を
以前本ブログで紹介した。前方駒が、取りた
い相手の駒の「途中の駒」になるのかどうか
が問題となり、排除円を1升目離れで視半径
42°にしたケースを当初考えたが、角道型
2枚並び駒の「穴」が、突き通せるかどうか
で、十数度回転しても穴が見えてしまい、ルー
ル複雑化するという事が判り、変更/調整を
余儀なくされた。その為当初の42°ルール
を44.5°ルールに変更した訳だが、
相手駒の角行と香車前方歩兵で、左米長玉が
突き刺せる程度に、複雑性を軽くしようとし
ていた所で、考察が止まっていた。
しかし、以下に述べるように、これでも、
途中2駒の斜め45°近い隙間から、超奔王
から取る駒が見えるのかどうかという点に関
して、ゲームの興味を損ねてしまう程度の煩
雑さが有る事が判明した。それは、次のよう
な図の例である。

上図で左下隅の超奔王は、5の5と6の4
の位置にある「手前駒相当」の2枚の歩兵が、
4の4と5の3よりも向こうに有るので、
間の穴が44.5°ルールで超奔王からは、
見え
それを通して、図で仮に、と金と成り香車が
い無いとすれば、以前に説明したように、
8の7位置の玉将が取りが掛かるのは、もち
ろんだが、今度は上図のような配列だとして、
8の6のと金は取れるのだが、7の7の成り
香車は取れ無いという、複雑さがある
のである。
ここで、問題なのは、
取れる駒が対角線から外れて、末広がりだと
いう面倒くささ
だと考えられる。
この事から、単一の駒に隠れるのかという
ルールなら我慢出切るが、
角道状の2つの駒の隙間の穴から、向こうの
駒が見えるのかという問題で、状態が複雑す
ぎると、ゲームとして興味は半減する可能性
が高い
と、本ブログの管理人には懸念される。
そこで、元に戻って単位升目離れた、間駒
の排除半径は、44.5°として、ちょうど
角道になる状態で1°の穴が突き通せるので
は無くて、45-δでδ→0の極限に、する
しか無いという考えに行き着く。
実は、遠方で排除円の視半径の距離に関す
る挙動が、升目数の42°ちょうどのの逆数
になるのではなく、本当は180/√2・π
=40.514236の逆数度になっている
に過ぎ無い。これまで逆比例の定数としてき
た、42°は、本当はarcCosec関数
挙動が厳密な為に、近傍で過大拡大して来る
ので大めに直し、かつ暗算が、やり易すくす
る為に、こうしているのに過ぎない。
特に逆数ではなくて、厳密にarc-
Cosec関数て角度を計算すると、1の0
か0の1の駒を見て視半径45°なら、
1の1は、厳格に30°なので、そうすれば
良く、
2の2、3の3・・・は、√2が1.4では
無くて、本当は1.41421356・・
なので、精度が問題になるときには答えを、
99%すれば良いという、例えば誤差となる。
2の0や0の2の駒は、42の逆数の21°
より、僅かに視半径は小さいはずである。そ
して、それ以遠の場合は、3%強程度、排除
半径を大きく見積もり過ぎているだけだろう。
以上の事から結論として、
0の1と1の0の駒は、排除半径45°、
1の1駒は同30°、その他は42°の升目
単位距離逆数の近似計算で、45°-δ但し
(δ→0)ルールは、問題は起こら無い
だろうと、推定される。
すると、そもそもいわゆる角道の時にしか、
前に有る2駒の隙間から、取る駒が見え無い
ルールに45-δルールではなると見られる。
ただし、桂馬走りルールは、そのままになる
はずである。これは、
それぞれの桂馬型引っかかり駒のカスリ断面
積のδ→0の極限が、角道穴の大きさの減少
の極限と、同次な無限小になる
と、私は思うからである。つまり現行の日本
将棋の角道ルールには、
角行の走り方向が45°の一定値なので良い
ものの、45°±δ(δ→0)だったとすれ
ば、数学的におかしな事になったという懸念
が有った
ようである。
ともかく、方位角がぴったり45°で無く
ても、角道型の穴が見えるという問題が、
隣升駒排除半径44.5°ルールではなくて、
45°-δ(δ→0)ルールにしてしまえば
無くなるので。今度こそは、超奔王有り将棋
ゲームは、問題無く指せるのてはないかと、
私には期待された。なお、以前述べたテスト
では、偶然だったが、今回述べたルールで、
ゲームの出来を、ほぼチェックしていたよう
である。山勘が当たりだったという事だろう。
(2023/10/22)
がアナログ角度で全てに亘る駒が一種類だけ
含まれる、日本将棋系の超奔王入り奔将棋を
以前本ブログで紹介した。前方駒が、取りた
い相手の駒の「途中の駒」になるのかどうか
が問題となり、排除円を1升目離れで視半径
42°にしたケースを当初考えたが、角道型
2枚並び駒の「穴」が、突き通せるかどうか
で、十数度回転しても穴が見えてしまい、ルー
ル複雑化するという事が判り、変更/調整を
余儀なくされた。その為当初の42°ルール
を44.5°ルールに変更した訳だが、
相手駒の角行と香車前方歩兵で、左米長玉が
突き刺せる程度に、複雑性を軽くしようとし
ていた所で、考察が止まっていた。
しかし、以下に述べるように、これでも、
途中2駒の斜め45°近い隙間から、超奔王
から取る駒が見えるのかどうかという点に関
して、ゲームの興味を損ねてしまう程度の煩
雑さが有る事が判明した。それは、次のよう
な図の例である。

上図で左下隅の超奔王は、5の5と6の4
の位置にある「手前駒相当」の2枚の歩兵が、
4の4と5の3よりも向こうに有るので、
間の穴が44.5°ルールで超奔王からは、
見え
それを通して、図で仮に、と金と成り香車が
い無いとすれば、以前に説明したように、
8の7位置の玉将が取りが掛かるのは、もち
ろんだが、今度は上図のような配列だとして、
8の6のと金は取れるのだが、7の7の成り
香車は取れ無いという、複雑さがある
のである。
ここで、問題なのは、
取れる駒が対角線から外れて、末広がりだと
いう面倒くささ
だと考えられる。
この事から、単一の駒に隠れるのかという
ルールなら我慢出切るが、
角道状の2つの駒の隙間の穴から、向こうの
駒が見えるのかという問題で、状態が複雑す
ぎると、ゲームとして興味は半減する可能性
が高い
と、本ブログの管理人には懸念される。
そこで、元に戻って単位升目離れた、間駒
の排除半径は、44.5°として、ちょうど
角道になる状態で1°の穴が突き通せるので
は無くて、45-δでδ→0の極限に、する
しか無いという考えに行き着く。
実は、遠方で排除円の視半径の距離に関す
る挙動が、升目数の42°ちょうどのの逆数
になるのではなく、本当は180/√2・π
=40.514236の逆数度になっている
に過ぎ無い。これまで逆比例の定数としてき
た、42°は、本当はarcCosec関数
挙動が厳密な為に、近傍で過大拡大して来る
ので大めに直し、かつ暗算が、やり易すくす
る為に、こうしているのに過ぎない。
特に逆数ではなくて、厳密にarc-
Cosec関数て角度を計算すると、1の0
か0の1の駒を見て視半径45°なら、
1の1は、厳格に30°なので、そうすれば
良く、
2の2、3の3・・・は、√2が1.4では
無くて、本当は1.41421356・・
なので、精度が問題になるときには答えを、
99%すれば良いという、例えば誤差となる。
2の0や0の2の駒は、42の逆数の21°
より、僅かに視半径は小さいはずである。そ
して、それ以遠の場合は、3%強程度、排除
半径を大きく見積もり過ぎているだけだろう。
以上の事から結論として、
0の1と1の0の駒は、排除半径45°、
1の1駒は同30°、その他は42°の升目
単位距離逆数の近似計算で、45°-δ但し
(δ→0)ルールは、問題は起こら無い
だろうと、推定される。
すると、そもそもいわゆる角道の時にしか、
前に有る2駒の隙間から、取る駒が見え無い
ルールに45-δルールではなると見られる。
ただし、桂馬走りルールは、そのままになる
はずである。これは、
それぞれの桂馬型引っかかり駒のカスリ断面
積のδ→0の極限が、角道穴の大きさの減少
の極限と、同次な無限小になる
と、私は思うからである。つまり現行の日本
将棋の角道ルールには、
角行の走り方向が45°の一定値なので良い
ものの、45°±δ(δ→0)だったとすれ
ば、数学的におかしな事になったという懸念
が有った
ようである。
ともかく、方位角がぴったり45°で無く
ても、角道型の穴が見えるという問題が、
隣升駒排除半径44.5°ルールではなくて、
45°-δ(δ→0)ルールにしてしまえば
無くなるので。今度こそは、超奔王有り将棋
ゲームは、問題無く指せるのてはないかと、
私には期待された。なお、以前述べたテスト
では、偶然だったが、今回述べたルールで、
ゲームの出来を、ほぼチェックしていたよう
である。山勘が当たりだったという事だろう。
(2023/10/22)







